طباعة الدرس

إجابات كتاب التمارين

مشتقة اقترانات خاصة

(1) يبين الشكل المجاور منحنى الاقتران f(x) . أحدد قيم x للنقاط التي يكون عندها الاقتران f(x) غير قابل للاشتقاق، مبرراً إجابتي.

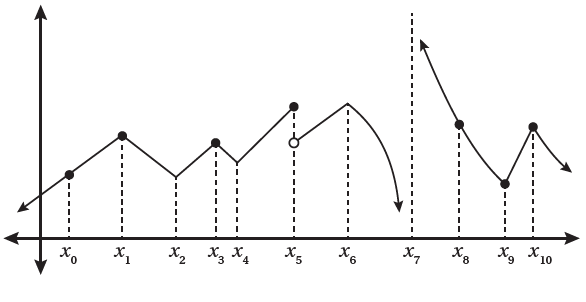
f غير قابل للشتقاق عند القيم x₁, x₂, x₃, x₄, x₆, x₉, x₁₀ بسبب وجود زاوية لمنحنى الاقتران عند كل منها رغم أنه متصل.

و f غير قابل للاشتقاق عند القيم x₅, x₇ وذلك لأنه غير متصل عندها، والاتصال شرط ضروري.

---

أجد مشتقة كل اقتران ممّا يأتي:

(2) f(x) = 9e^x + $\frac{1}{\sqrt[3]{x}}$

f(x) = 9e^x + $\frac{1}{3}$$x^{-\frac{1}{2}}$

f ’(x) = 9e^x - $\frac{1}{6}$$x^{-\frac{3}{2}}$ = 9e^x - $\frac{1}{6\sqrt{x^3}}$

(3) f(x) =  2e^x + $\frac{1}{x^2}$

f(x) =  2e^x + x^-2

f ’(x) =  2e^x - 2x^-3 =  2e^x - $\frac{2}{x^3}$

(4) f(x) = $\frac{\mathrm{\pi }}{2}$ sin x – cos x

f ’(x) = $\frac{\mathrm{\pi }}{2}$ cos x + sin x

---

(5) أجد معادلة المماس لمنحنى الاقتران: f(x) 2e^x + x عندما x = 2 .

f(x) =  2e^x + x   ,   x = 2

f(2) =  2e² + 2  

f ’(x) = 2e^x  + 1

ميل المماس:

f ’(2) = 2e² + 1

معادلة المماس:

y – 2e² – 2 = (2e² + 1) (x – 2)

y =  (2e² + 1) x – 2e²

---

(6) أثبت عدم وجود مماس أفقي لمنحنى الاقتران: f(x) = 3x + sin x + 2 .

f ’(x) = 3 + cos x

عند المماس الأفقي يكون f ’(x) = 0

3 + cos x = 0  →  cos x = -3

وهذه المعادلة ليس لها حلّ؛ لأن -1$\le$cos x $\le$1

إذن، لا توجد مماسات أفقية لمنحنى f .

---

يمثل الاقتران: s(t) = 3t² – t³ , t $\mathbf{\ge }$0 موقع جُسيم يتحرّك في مسار مستقيم، حيث s الموقع بالأمتار، و t الزمن بالثواني:

(7) أجد سرعة الجسيم وتسارعه بعدt  ثانية.

s(t) = 3t² – t³   ,  t $\ge$0

السرعة:

v(t) = 6t – 3t²

التسارع:

a(t) = 6 – 6t

 

(8) أجد الموقع (المواقع) الذي يكون عنده الجُسيم في حالة سكون لحظي.

يكون الجُسيم في حالة سكون لحظي عندما v(t) = 0

v(t) = 6t – 3t² = 0  $\Rightarrow$ 3t(2 – t) = 0  $\Rightarrow$  t = 0  ,  t = 2

s(0) = 0, s(2) = 12 – 8 = 4

إذن يكون الجُسيم في حالة سكون لحظي عندما يكون في كل من الموقعين:

s = 0 m    ,    s = 4 m

---

إذا كان: f(x) = ln x² ، حيث x > 0 ، فأجيب عن السؤالين الآتيين تباعاً:

(9) أجد معادلة مماس منحنى الاقتران عندما x = e² .

f(x) =  ln x² = 2 ln x   ,   x = e²

f(e²) = 2 ln e² = 4   $\Rightarrow$ (e² , 4)

f ’(x) = $\frac{2}{x}$

ميل المماس:

f ’(e²) = $\frac{2}{e^2}$

معادلة المماس:

y – 4 = $\frac{2}{e^2}$ (x – e²)  $\Rightarrow$  y = $\frac{2}{e^2}$ x + 2

(10) أجد الإحداثي x للنقطة التي يكون المماس عندها موازياً للمستقيم 6x – 2y + 5 = 0

ميل المستقيم الذي معادلته 6x – 2y + 5 = 0 يساوي 3

f ’(x) = $\frac{2}{x}$ = 3  $\Rightarrow$ x = $\frac{2}{3}$

---

إذا كان: f(x) = 2 sin x – 4 cos x ، فأجيب عن السؤالين الآتيين تباعاً:

(11) أجد ميل المماس لمنحنى الاقتران f(x) عندما x = 0 .

f ’(x) = 2 cos x + 4 sin x

f ’(0) = 2 cos 0 + 4 sin 0 = 2

(12) أجد معادلة المماس لمنحنى الاقتران f(x) عندما x = $\frac{\mathrm{\pi }}{2}$ .

نجد الإحادثي y عندما x = $\frac{\mathrm{\pi }}{2}$  

f ($\frac{\mathrm{\pi }}{2}$) = 2 sin $\frac{\mathrm{\pi }}{2}$ - 4 cos $\frac{\mathrm{\pi }}{2}$ = 2

 ميل المماس:

f ’($\frac{\mathrm{\pi }}{2}$) = 2 cos $\frac{\mathrm{\pi }}{2}$ + 4 sin $\frac{\mathrm{\pi }}{2}$ = 4

معادلة المماس:

y - 2 = 4 (x - $\frac{\mathrm{\pi }}{2}$)  $\Rightarrow$ y = 4x – 2π + 2