طباعة الدرس

إجابات كتاب التمارين

احتمال المتغير العشوائي الطبيعي باستعمال الجدول

إذا كان $\mathit{X}$ متغيراً عشوائياً طبيعياً، وسطه الحسابي 89، وانحرافه المعياري 11.5، فأجد القيمة المعيارية $\mathit{z}$ التي تقابل قيمة $\mathit{x}$ في كل مما يأتي:

$x=81$ (1)

$z=\frac{81-89}{11.5}=-\frac{16}{23}$

$x=92$ (2)

$z=\frac{92-89}{11.5}=\frac{6}{23}$

$x=100$ (3)

$z=\frac{100-89}{11.5}=\frac{22}{23}$

إذا كان $\mathit{X}$ متغيراً عشـوائياً طبيعياً، وسطه الحسابي 220، وانحرافه المعياري 10، فأجد قيمة $\mathit{x}$ التي تقابل القيمة المعيارية $\mathit{z}$ في كل مما يأتي:

$z=2$ (4)

$\frac{x-220}{10}=2\Rightarrow x=240$

$z=-3.5$ (5)

$\frac{x-220}{10}=-3.5\Rightarrow x=185$

$z=4.2$ (6)

$\frac{x-220}{10}=4.2\Rightarrow x=262$

إذا كان: $\mathit{X}\mathbf{~}\mathit{N}\mathbf{(}\mathbf{17}\mathbf{,}\mathbf{100}\mathbf{)}$، فأجد كل احتمال مما يأتي، مستعملاً جدول التوزيع الطبيعي المعياري:

$P(X<25.8)$ (7)

$\begin{array}{rl}P(X<25.8)& =P(Z<\frac{25.8-17}{10})\\ & =P(Z<0.88)=0.8106\end{array}$

$P(X>10.5)$ (8)

$\begin{array}{rl}P(X>10.5)& =P(Z>\frac{10.5-17}{10})\\ & =P(Z>-0.65)\\ & =P(Z<0.65)=0.7422\end{array}$

$P(19.4<X<30.2)$ (9)

$\begin{array}{rl}P(19.4<X<30.2)& =P(\frac{19.4-17}{10}<Z<\frac{30.2-17}{10})\\ & =P(0.24<Z<1.32)\\ & =P(Z<1.32)-P(Z<0.24)\\ & =0.9066-0.5948=0.3118\end{array}$

$P(4<X<17)$ (10)

$\begin{array}{rl}P(4<X<17)& =P(\frac{4-17}{10}<Z<\frac{17-17}{10})\\ & =P(-1.3<Z<0)\\ & =P(Z<0)-P(Z<-1.3)\\ & =0.5-(1-P(Z<1.3\left)\right)\\ & =0.5-(1-0.9032)=0.4032\end{array}$

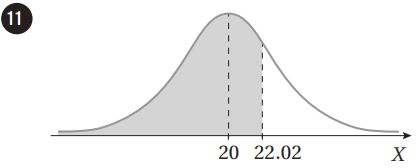
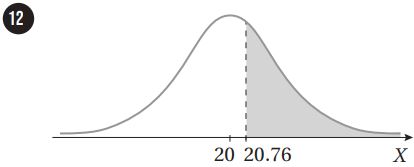
إذا كان: $\mathit{X}\mathbf{~}\mathit{N}\mathbf{(}\mathbf{20}\mathbf{,}\mathbf{9}\mathbf{)}$، فأجد مساحة المنطقة المظللة أسفل منحنى التوزيع الطبيعي للمتغير العشوائي $\mathit{X}$ في كل مما يأتي:

$P(X<22.02)=P(Z<\frac{22.02-20}{3})=P(Z<0.67)=0.7486$

$\begin{array}{rl}P(X>20.76)& =P(Z>\frac{20.76-20}{3})\\ & =P(Z>0.25)\\ & =1-P(Z<0.25)\\ & =1-0.5987=0.4013\end{array}$

رياضة: تتبع أطوال لاعبي كرة السلة توزيعاً طبيعياً، وسطه الحسابي 185cm، وانحرافه المعياري 5cm. إذا اختير لاعب عشوائياً، فأجد كلاً مما يأتي:

(13) احتمال أن يزيد طول اللاعب على 175cm 

$\begin{array}{rl}P(X>175)& =P(Z>\frac{175-185}{5})\\ & =P(Z>-2)\\ & =P(Z<2)\\ & =0.9772\end{array}$

(14) احتمال أن يتراوح طول اللاعب بين 180cm و 190cm

$\begin{array}{rl}P(180<X<190)& =P(\frac{180-185}{5}<Z<\frac{190-185}{5})\\ & =P(-1<Z<1)\\ & =P(Z<1)-P(Z<-1)\\ & =P(Z<1)-(1-P(Z<1\left)\right)\\ & =2P(Z<1)-1\\ & =2\left(0.8413\right)-1=0.6826\end{array}$

(15) العدد التقريبي للاعبين الذين تزيد أطوالهم على 195cm من بين 2000 لاعب.

$\begin{array}{rl}& P(X>195)=P(Z>\frac{195-185}{5})\\ & =P(Z>2)\\ & =1-P(Z<2)\\ & =1-0.9772=0.0228\\ & N=0.0228\times 2000=45.6\approx 46\end{array}$