طباعة الدرس

إجابات أتحقق من فهمي

الاقترانات المثلثية

الاقترانات المثلثية

أتحقق من فهمي صفحة (20):

أجد قيم الاقترانات المثلثية الستة للزاوية Ɵ في المثلث المجاور.

$\begin{array}{rl}& x=\sqrt{49-25}=\sqrt{24}\\ & sin\theta =\frac{5}{7} ,cos\theta =\frac{\sqrt{24}}{7} ,tan\theta =\frac{5}{\sqrt{24}}\\ & csc\theta =\frac{7}{5} ,sec\theta =\frac{7}{\sqrt{24}} ,cot\theta =\frac{\sqrt{24}}{5}\end{array}$

---

قيم الاقترانات المثلثية لأيّ زاوية باستعمال نقطة معلومة

أتحقق من فهمي صفحة (21):

تقع النقطة (1, -3) على ضلع انتهاء الستة الزاوية Ɵ المرسومة في الوضع القياسي. أجد قيم الاقترانات المثلثية الستة للزاوية Ɵ.

$\begin{array}{rl}& r=\sqrt{1+9}=\sqrt{10}\\ & sin\theta =\frac{-3}{\sqrt{10}} ,cos\theta =\frac{1}{\sqrt{10}} ,tan\theta =-3 ,\\ & csc\theta =\frac{-\sqrt{10}}{3} ,sec\theta =\sqrt{10 } ,cot\theta =\frac{-1}{3}\end{array}$

---

إيجاد قيم الاقترانات المثلثية للزوايا الربعية

أتحقق من فهمي صفحة (23):

أجد قيم كل اقتران مثلثي ممّا يأتي إذا كان مُعرّفاً. وإلا أكتب عبارة (غير مُعرّف):

a) sin 3π

sin 3π = $\frac{0}{1}$ = 0

b) tan 90^o

tan 90^o = $\frac{1}{0}$ (غير معرف)

c)  sec (- $\frac{3\mathrm{\pi }}{2}$)

sec $\frac{-3\mathrm{\pi }}{2}$ = $\frac{1}{0}$ (غير معرف)

---

إيجاد قيم الاقترانات المثلثية باستعمال الزوايا المرجعية

أتحقق من فهمي صفحة (26):

أجد قيمة كلّ ممّا يأتي:

a) sin 210^o

$sin {210}^{\circ }=-sin {30}^{\circ }=-0.5$

b) cos 510^o

$\cos {510}^{\circ }=-\cos {30}^{\circ }=-\frac{\sqrt{3}}{2}$

c) sec 5 π

$\sec 5\pi =\sec \pi =-1$

d) tan (- $\frac{2\mathrm{\pi }}{3}$)

$\tan -\frac{2\pi }{3}=-\tan \frac{2\pi }{3}=\sqrt{3}$

 

أتحقق من فهمي صفحة (27):

إذا كان sec Ɵ = 2 ، حيث sin Ɵ < 0 ، فأجد قيمة كلّ من الاقترانات المثلثية الخمسة المتبقية للزاوية Ɵ . 

$sin\theta =-\frac{\sqrt{3}}{2} , cos \theta =\frac{1}{2}, tan \theta =-\sqrt{3} , csc\theta =-\frac{2}{\sqrt{3}} , cot \theta =-\frac{1}{\sqrt{3}}$

 

أتحقق من فهمي صفحة (27):

أجد الزمن الذي تستغرقه عملية الانزلاق على منحدر طوله 3000 ft ، وزاوية ميله $\frac{\mathrm{\pi }}{4}$ ، مُستعملاً العلاقة الواردة في المثال 6 .

$t=\frac{\sqrt{dcsc\theta }}{4}=\frac{\sqrt{3000csc\frac{\pi }{4}}}{4}=\frac{\sqrt{3000\frac{\sqrt{2}}{2}}}{4}=\frac{5\sqrt{15\sqrt{2}}}{2}\approx 11.51\mathrm{s}$

---

معكوس اقتران الجيب، وجيب التمام، والظل

أتحقق من فهمي صفحة (30):

أجد قيمة كلّ ممّا يأتي (إن وجدت):

a) ${\sin }^{-1} \frac{1}{\sqrt{2}}$

$si{n}^{-1} \frac{1}{\sqrt{2}}=\frac{\pi }{4}$

b) cos^-1 0

${\cos }^{-1} 0=\frac{\pi }{2}$

c) ${\tan }^{-1} (-\frac{1}{\sqrt{3}})$

${\tan }^{-1} \frac{-1}{\sqrt{3}}=-\frac{\pi }{6}$

 

أتحقق من فهمي صفحة (31):

إذا كات مساحة القطاع الدائري OAB هي 164 cm² في الشكل المجاور، فأجد مساحة OABΔ .

$\begin{array}{rl}& A=\frac{1}{2}{r}^2\theta \to \frac{1}{2}(20{)}^2\theta =164\to \theta =\frac{41}{50}\mathrm{rad}\\ & \frac{1}{2}(20{)}^{2}sin \frac{41}{50}\approx 146.3{\mathrm{cm}}^2\end{array}$

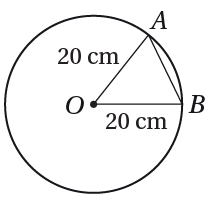
مساحة المثلث = نصف حاصل ضرب طولي ضلعي فيه بجيب الزاوية المحصورة بينهما.