أتدرب وأحل المسائل
الضرب القياسي
أجد ناتج الضرب القياسي للمتجهين في كل مما يأتي:
(1)
(2)
(3)
(4)
أجد قياس الزاوية بين المتجهين إلى أقرب عشر درجة في كل مما يأتي:
(5)
(6)
(7) إذا كانت وO نقطة الأصل، فأجد إلى أقرب درجة.
(8) يمر المستقيم بالنقطتين: ، ويمر المستقيم بالنقطتين: أجد قياس الزاوية الحادة بين المستقيم والمستقيم إلى أقرب عشر درجة.
اتجاه المستقيم هو:
اتجاه المستقيم هو:
إذن، قياس الزاوية الحادة بين المستقيمين و هو تقريباً.
(9) إذا كان المستقيم الذي له المعادلة المتجهة: ، والمستقيم الذي له المعادلة المتجهة: متعامدين، فما القيم الممكنة للثابت q؟
اتجاه المستقيم الأول هو:
اتجاه المستقيم الثاني هو:
المستقيمان متعامدان، فاتجاههما متعامدان، أي أن:
إذا كانت: معادلة متجهة للمستقيم ، والنقطة غير واقعة على المستقيم ، فأجيب عن السؤالين الآتيين تباعاً:
(10) أحدد مسقط العمود من النقطة P على المستقيم .
لتكن هي المسقط العمودي للنقطة على المستقيم ، فإن متجه موقعها هو:
إذا كان هو العمود من على المستقيم ، فإن:
بما أن يعامد ، إذن:
إذن، مسقط العمود على المستقيم هو
(11) أجد البعد بين النقطة P والمستقيم .
(12) أجد مساحة المثلث ABC، حيث: .
ليكن قياس الزاوية
(13) أجد مساحة المثلث ABC الذي إحداثيات رؤوسه هي: .
ليكن قياس الزاوية
 (14) حزام ناقل: يمثل المتجه: القوة التي يولدها حزام ناقل لتحريك حقيبة في مسار مستقيم، من النقطة إلى النقطة . أجد مقدار الشغل الذي تبذله القوة F، علماً بأن القوة بالنيوتن N، والمسافة بالمتر m، ومقدار الشغل (W) المبذول بوحدة الجول (J) يساوي ناتج الضرب القياسي لمتجه القوة في متجه الإزاحة؛ أي: .
(14) حزام ناقل: يمثل المتجه: القوة التي يولدها حزام ناقل لتحريك حقيبة في مسار مستقيم، من النقطة إلى النقطة . أجد مقدار الشغل الذي تبذله القوة F، علماً بأن القوة بالنيوتن N، والمسافة بالمتر m، ومقدار الشغل (W) المبذول بوحدة الجول (J) يساوي ناتج الضرب القياسي لمتجه القوة في متجه الإزاحة؛ أي: .
(15) إذا كانت النقطة ، والنقطة تقعان على المستقيم ، وكانت النقطة Q تقع على المستقيم ، حيث عمودي على ، فأجد متجه الموقع للنقطة Q.
إذن، يمكن تبسيط اتجاه المستقيم بقسمة على 4:
معادلة المستقيم هي:
النقطة هي المسقط العمودي للنقطة على هذا المستقيم، فيكون متجه موقعها هو:
بما أن و متعامدان، فإن:
إذا كانت متجهات مواقع النقاط: A، وB، وC هي: على الترتيب، فأجيب عن الأسئلة الأربعة الآتية تباعاً:
(16) أثبت أن: .
(17) أجد متجه موقع النقطة C إذا كان ABCD مستطيلاً.
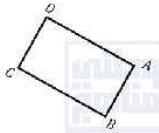 ارسم شكل مستوي تقريبي يوضح المسألة (المهم ترتيب رؤوس المستطيل بالتوالي مع عقارب الساعة أو عكس عقارب الساعة)، أينما كان موقع O، فإن:
ارسم شكل مستوي تقريبي يوضح المسألة (المهم ترتيب رؤوس المستطيل بالتوالي مع عقارب الساعة أو عكس عقارب الساعة)، أينما كان موقع O، فإن:
(ويمكن إيجاد عبر الرأس من العلاقة: )
(18) أجد مساحة المستطيل ABCD.
إذن، مساحة تساوي 540 وحدة مربعة.
(19) أجد متجه موقع مركز المستطيل ABCD.
مركز المستطيل هي نقطة تقاطع قطريه وهي نقطة منتصف كل من القطرين. نأخذ القطر ولتكن نقطة منتصفه ، فإن:
تمثل: معادلة متجهة للمستقيم ، وتُمثل: معادلة متجهة للمستقيم ، وتمثل: معادلة متجهة للمستقيم .
إذا تقاطع المستقيم والمستقيم في النقطة T، وكانت النقطة F تقع على المستقيم ، حيث: ، فأجيب عن السؤالين الآتيين تباعاً:
(20) أجد إحداثيات النقطة F.
لإيجاد نقطة تقاطع نساوي في معادلتهما ونساوي الإحداثيات المتناظرة:
بتعويض في المعادلتين (1) و(2) نجد أن
لإيجاد إحداثيات نقطة التقاطع نعوض في معادلة
إذن، نقطة تقاطع هي
هو المسقط العمودي للنقطة على ، إذن:
اتجاه هو
لكن يعامد إذن،
(21) أجد البعد بين النقطة T والمستقيم .
إذا كانت: معادلة متجهة للمستقيم ، وكانت ، فأجيب عن السؤالين الآتيين تباعاً:
(22) أجد قياس الزاوية الحادة بين المستقيم والمستقيم .
وهذا هو اتجاه المستقيم
اتجاه المستقيم هو:
(23) تقع النقطة C على المستقيم ، حيث: AB=AC. أجد إحداثيات النقطة C.
بما أن عى استقامة واحدة، و إذن، هي نقطة منتصف حيث:
إذن، أحداثيات النقطة هي:
تقع النقطة والنقطة على المستقيم ، وتقع النقطة على المستقيم الذي معادلته: :
(24) أبين أن النقطة B تقع على المستقيم .
متجه موقع أي نقطة على يكون
حتى تقع على ينبغي وجود قيمة تحقق المعادلة:
لهذه المعدلات الثلاث الحل نفسه
إذن، تقع على المستقيم لأنها تنتج من تعويض في معادلته.
(25) أبين أن المستقيم والمستقيم متعامدان.
اتجاه هو:
ويمكن تبسيطه إلى
اتجاه هو:
إذن، المستقيمان متعامدان.
(26) أجد .
بما أن متعامدان، ونقطة التقائهما هي (كونها واقعة على كل منهما كما سبق)
إذن،
(27) أجد مساحة المثلث ABC.
المثلث قائم في
إذن، مساحة المثلث تسلوي 69.2 وحدة مربعة تقريباً.
ABCD هرم ثلاثي. إذا كانت إحداثيات رؤوسه هي: فأجيب عن الأسئلة الثلاثة الآتية تباعاً:
(28) أجد مساحة المثلث ABC في صورة: .
ليكن قياس الزاوية
(29) أثبت أن: ، حيث .
إذن، وقياس الزاوية هو .
(30) إذا علمت أن النقطة E تقع في المستوى نفسه الذي يقع فيه المثلث ABC، فأجد حجم الهرم ABCD.
ويمثل ارتفاع ، أما مساحة قاعدته ، وذلك من السؤال 28 ، إذن حجم الهرم هو:
إذن حجم الهرم يساوي 126 وحدة مكعبة.
إذا كانت ، فأجيب عن الأسئلة الخمسة الآتية تباعاً:
(31) أبين أن : ، حيث n عدد صحيح.
تكون قيمة هي 5
(32) أبين أن قياس الزاوية ACB هو .
ليكن قياس الزاوية
(33) أكتب معادلة متجهة للمستقيم .
ويمكن التعبير عن اتجاه المستقيم بالمتجه
وتكون معادلته:
(34) إذا كانت ، وعُلم أن ، متقاطعان، فما قيمة p؟
ويمكن التعبير عن اتجاه المستقيم بالمتجه
معادلة :
يتقاطع المستقيمان، إذن، يوجد u,t بحيث تتساوى لهما في المعادلتين:
بجمع المعادلتين (1) و(2)، نجد أن: ثم بالتعويض في (3) نجد أن:
(35) أبين أن الشكل ABCD معين، ثم أجد طول كل ضلع من أضلاعه.
من (1) و(2) ينتج أن الشكل ABCD متوازي أضلاع، والآن نجد طول
وبما أن ABCD متوازي أضلاع فيه ضلعان متجاوران متطابقان فهو معين جميع أضلاعه متطابقة طول كل واحد منها 7 وحدات.
(36) أحل المسألة الواردة في بداية الدرس.
تم حل هذا السؤال في موضعه تحت عنوان "مسألة اليوم".


النقاشات