أتحقق من فهمي
تطبيقات القيم القصوى
إيجاد أكبر حجم ممكن
أتحقق من فهمي صفحة 121
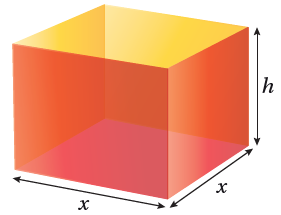 ترغب شركة في تصميم صندوق مفتوح من الأعلى، وقاعدته مربعة الشكل، ومساحة سطحه الكلية 1080 cm2 كما في الشكل المجاور. أجد أبعاد الصندوق ليكون حجمه أكبر ما يمكن.
ترغب شركة في تصميم صندوق مفتوح من الأعلى، وقاعدته مربعة الشكل، ومساحة سطحه الكلية 1080 cm2 كما في الشكل المجاور. أجد أبعاد الصندوق ليكون حجمه أكبر ما يمكن.
ليكن حجم الصندوق V ومساحة سطحه الكلية A
القيمة الحرجة هي:
أجد حجم الصندوق عند القيمة الحرجة وعند طرفي المجال.
إذن يكون الحجم أكبر ما يمكن عندما وعندها يكون الارتفاع
إيجاد أقل طول ممكن
أتحقق من فهمي صفحة 124
 خطط مزارع لتسييج حضيرة مستطيلة الشكل قرب نهر كما في الشكل المجاور، وحدّد مساحة الحظيرة بـ 245000 m2 ؛ لتوفير كمية عشب كافية لأغنامه.
خطط مزارع لتسييج حضيرة مستطيلة الشكل قرب نهر كما في الشكل المجاور، وحدّد مساحة الحظيرة بـ 245000 m2 ؛ لتوفير كمية عشب كافية لأغنامه.
أجد أبعاد الحظيرة التي تجعل طول السياج أقل ما يمكن، علماً بأنّ الجزء المقابل للنهر لا يحتاج إلى تسييج.
ليكن طول السياج L ومساحة الحظيرة A
قيمة x الحرجة هي: 700
إذن يكون طول السياج أقل ما يمكن عندما x = 700 m و
إيجاد أقرب مسافة
أتحقق من فهمي صفحة 126
 انطلق قطار من إحدى المحطات الساعة 10:00 a.m. ، وتحرك في اتجاه الجنوب بسرعة 60 km/h ، حيث المحطة التالية. وفي الوقت نفسه، انطلق قطار آخر نحو الغرب بسرعة 45 km/h ، ثم وصل إلى محطة الأول الساعة 11:00 a.m. . في أي ساعة يكون القطاران أقرب ما يمكن إلى بعضهما؟
انطلق قطار من إحدى المحطات الساعة 10:00 a.m. ، وتحرك في اتجاه الجنوب بسرعة 60 km/h ، حيث المحطة التالية. وفي الوقت نفسه، انطلق قطار آخر نحو الغرب بسرعة 45 km/h ، ثم وصل إلى محطة الأول الساعة 11:00 a.m. . في أي ساعة يكون القطاران أقرب ما يمكن إلى بعضهما؟
نفرض x بُعد القطار الأول عن المحطة، y بُعد القطار الثاني عن المحطة، ونفرض D البعد بين القطارين.
القطار الثاني استغرق ساعة واحدة للوصول إلى المحطة، إذن فقد انطلق من نقطة تبعد 24 كيلومتراً عنها.
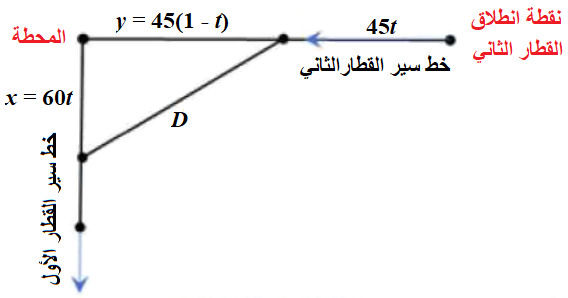
بعد t ساعة من انطلاقهما يكون: ، ويكون
القيمة الحرجة هي:
أجد المسافة D عند القيمة الحرجة وعند طرفي المجال.
إذن يكون القطاران أقرب ما يمكن إلى بعضهما عندما ، أي بعد 21 دقيقة و 36 ثانية، وتكون الساعة حينئذ 10:21:36
تطبيقات اقتصادية
أتحقق من فهمي صفحة 128
 يبيع متجر 200 شاشة تلفاز شهرياً بسعر JD 350 للشاشة الواحدة. وقد أشار مسح للسوق أعدّه خبير التسويق في المتجر إلى أن عدد الشاشات المبيعة شهرياً يزيد بمقدار 20 شاشة عند كل خصم مقداره JD 10 من سعر الشاشة الواحدة. أجد سعر بيع الشاشة الواحدة الذي يحقق للمتجر أعلى إيراد ممكن.
يبيع متجر 200 شاشة تلفاز شهرياً بسعر JD 350 للشاشة الواحدة. وقد أشار مسح للسوق أعدّه خبير التسويق في المتجر إلى أن عدد الشاشات المبيعة شهرياً يزيد بمقدار 20 شاشة عند كل خصم مقداره JD 10 من سعر الشاشة الواحدة. أجد سعر بيع الشاشة الواحدة الذي يحقق للمتجر أعلى إيراد ممكن.
ليكن سعر بيع الشاشة الواحدة هو x دينار.
أي أن مقدار الخصم من سعر بيع الشاشة الواحدة هو 350 - x دينار، وبالتالي تحصل زيادة في عدد الشاشات المبيعة مقدارها شاشة.
إذن عدد الشاشات المبيعة سيكون: 200 + 700 – 2x = 900 – 2x
الإيراد = عدد الشاشات المبيعة × سعر بيع الشاشة الواحدة بعد الخصم:
توجد قيمة حرجة وحيدة هي: 225
نلاحظ أن اقتران الإيراد له قيمة عظمى عندما x = 225
إذن يحقق المتجر أعلى إيراد ممكن عندما يكون سعر بيع الشاشة الواحدة هو 225 ديناراً.
إيجاد أكبر زاوية
أتحقق من فهمي صفحة 129
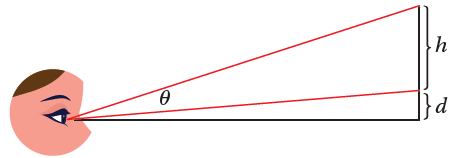 نظرت سارة إلى لوحة معلقة على حائط منزلها ارتفاعها h متراً وارتفاع حافتها السفلية d متراً فوق عينها كما في الشكل المجاور. كم متراً يجب أن تبتعد سارة عن الجدار لتكون زاوية نظرها Ɵ أكبر ما يمكن؟
نظرت سارة إلى لوحة معلقة على حائط منزلها ارتفاعها h متراً وارتفاع حافتها السفلية d متراً فوق عينها كما في الشكل المجاور. كم متراً يجب أن تبتعد سارة عن الجدار لتكون زاوية نظرها Ɵ أكبر ما يمكن؟
نسمي الأبعاد وقياسات الزوايا كما في الشكل:
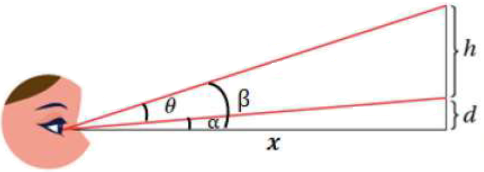
بما أّن ، فإن ، إذن
توجد قيمة حرجة وحيدة هي:
نستخدم اختبار المشتقة الأولى، وندرس إشارة
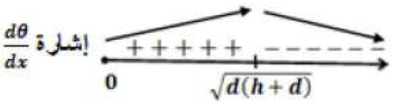
أعوض
أعوض
إذن يجب أن تبتعد سارة عن الجدار مسافة لتكون زاوية نظرها Ɵ أكبر ما يمكن.
تطبيقات في المستوى الإحداثي
أتحقق من فهمي صفحة 131
أجد النقطة (النقاط) الواقعة على منحنى الاقتران: ، التي هي أقرب ما يُمكن إلى النقطة (4, 2).
لتكن النقطة (x, y) على منحنى ، ولتكن المسافة بينها وبين النقطة (4, 2) هي L حيث:
نستخدم اختبار المشتقة الأولى وندرس إشارة
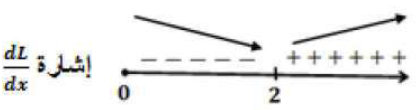
إذن أقرب نقطة من نقاط المنحنى f للنقطة (4, 2) هي: (2, 4).
إعداد : شبكة منهاجي التعليمية
25 / 11 / 2022
النقاشات