مهارات التفكير العليا

مهارات التفكير العليا

المتجهات في الفضاء

(41) أكتشف الخطأ: قالت حنان: "إذا كانت النقطة $A (7, - 3, 3)$ تقع على كرة مركزها نقطة الأصل، فإن النقطة $B (2, - 8, - 1)$ تقع خارج هذه الكرة"، في حين قالت هديل: "النقطة B تقع داخل هذه الكرة"، أيّ القولين صحيح، مبرراً إجابتي.

بما أن مركز الكرة هو $O (0, 0, 0)$ والنقطة $A (7, - 3, 3)$ تقع عليه فإن طول نصف قطرها R حيث:

$\begin{aligned} R = O A = \sqrt{(7 - 0)^{2} + (- 3 - 0)^{2} + (3 - 0)^{2}} = \sqrt{49 + 9 +} \\ O B = \sqrt{(2 - 0)^{2} + (- 8 - 0)^{2} + (- 1 - 0)^{2}} = \sqrt{4 + 64 + 1} \end{aligned}$

بما أن $O B > R$ فإن النقطة B تقع خارج الكرة، ويكون قول حنان هو الصواب.

(42) تبرير: إذا وقعت النقطة $J (- 4, 6, - 1)$ والنقطة $K (- 2, 2, 17)$ على طرفي أحد أقطار كرة، فأبين أن النقطة $L (2, 10, 3)$ والنقطة $J (4, - 2, 7)$ تقعان على سطح تلك الكرة، مبرراً إجابتي.

مركز الكرة هو النقطة C التي تنصف القطر المعطى طرفاه:

$C = (\frac{- 4 - 2}{2}, \frac{6 + 2}{2}, \frac{- 1 + 17}{2}) = (- 3, 4, 8)$

وطول نصف قطر الكرة هو R حيث:

$R = C K = \sqrt{(- 3 - (- 2))^{2} + (4 - 2)^{2} + (8 - 17)^{2}} = \sqrt{1 + 4 + 81} = \sqrt{86}$

الآن نجد كلاً من $C J, C L$ ونقارنه مع R لمعرفة موقع كل من J,L بالنسبة لهذه الكرة:

$C L = \sqrt{(2 - (- 3)^{2} + (10 - 4)^{2} + (3 - 8)^{2}} = \sqrt{25 + 36 + 25} = \sqrt{86} = R$

إذن، النقطة L أيضاً تقع على سطح هذه الكرة.

$C J = \sqrt{(4 - (- 3))^{2} + (- 2 - 4)^{2} + (7 - 8)^{2}} = \sqrt{49 + 36 + 1} = \sqrt{86} = R$

إذن، النقطة J أيضاً تقع على سطح هذه الكرة.

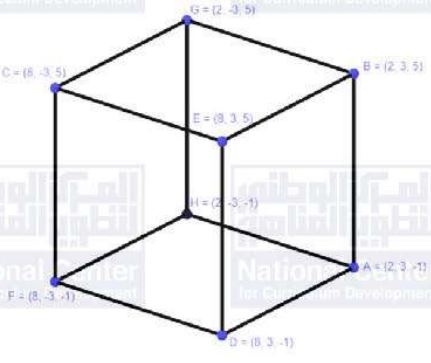
(43) تبرير: تمثل النقاط: $A (2, 3, - 1), B (2, 3, 5), C (8, - 3, 5)$ ثلاثة من رؤوس مكعب خشبي، كل وجهين من أوجهه يوازيان أحد المستويات: $x y, x z, y z$ .

أكتب إحداثيات الرؤوس الخمسة الأخرى، مبرراً إجابتي.

تختلف النقطة B عن النقطة A فقط في الإحداثي z، والفرق بين قيمتي z يساوي 6

إذن، AB أحد أحرف المكعب، وطول ضلع المكعب 6 وحدات.

أما النقطة C فيزيد إحداثيها x بمقدار 6 وحدات عن الإحداثي x للنقطة B، كما يقل إحداثيها y بمقدار 6 عن الإحداثي y للنقطة B (مزاحة عنها 6 وحدات لليسار).

نجد باقي النقاط (الرؤوس) بإحداث إزاحات مقدارها 6 وحدات لإحداثيات الرؤوس الثلاثة المعطاة.

$D (8, 3, - 1)$ وذلك بإزاحة النقطة A بمقدار 6 وحدات باتجاه المحور x الموجب.

$E (8, 3, 5)$ وذلك بإزاحة النقطة B بمقدار 6 وحدات باتجاه المحور x الموجب.

$F (8, - 3, - 1)$ وذلك بإزاحة النقطة C بمقدار 6 وحدات باتجاه المحور z السالب.

$G (2, - 3, 5)$ وذلك بإزاحة النقطة B بمقدار 6 وحدات باتجاه المحور y السالب.

$H (2, - 3, - 1)$ وذلك بإزاحة النقطة A بمقدار 6 وحدات باتجاه المحور y السالب.

حل 43

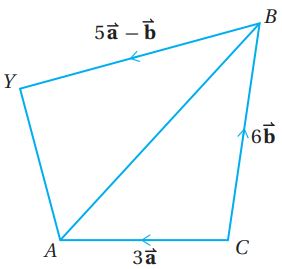
(44) تحد: في الشكل الآتي، إذا كان: $\vec{C B} = 6 \vec{b}, \vec{B Y} = 5 \vec{a} - \vec{b}, \vec{C A} = 3 \vec{a}$ ، وكانت X تقع على $\bar{A B}$ ، حيث $A X : X B = 1 : 2$ ، فأثبت أن: $\vec{C X} = \frac{2}{5} \vec{C Y}$ .

$\begin{aligned} \frac{A X}{X B} = \frac{1}{2} \Rightarrow X B = 2 A X \Rightarrow A B = A X + X B = A X + 2 A X = 3 A X \\ \Rightarrow A X = \frac{1}{3} A B \\ \vec{A X} = \frac{1}{3} \vec{A B} = \frac{1}{3} (\vec{A C} + \vec{C B}) = \frac{1}{3} (- 3 \vec{a} + 6 \vec{b}) = - \vec{a} + 2 \vec{b} \\ \vec{C Y} = \vec{C B} + \vec{B Y} = 6 \vec{b} + 5 \vec{a} - \vec{b} = 5 (\vec{a} + \vec{b}) \Rightarrow \vec{a} + \vec{b} = \frac{1}{5} \vec{C Y} \\ \vec{C X} = \vec{C A} + \vec{A X} = 3 \vec{a} - \vec{a} + 2 \vec{b} = 2 (\vec{a} + \vec{b}) = \frac{2}{5} \vec{C Y} \end{aligned}$

تحد: إذا كانت متجهات الموقع للنقاط: $M, L, N$ هي:

$\vec{m} = - 3 \hat{i} - 6 \hat{j} + \hat{k}, \vec{l} = 4 \hat{i} - 10 \hat{j} + 3 \hat{k}, \vec{n} = 5 \hat{i} + 3 \hat{j} - 9 \hat{k}$ ، فأجيب عن السؤالين الآتيين تباعاً:

(45) أثبت أن المثلث LMN قائم الزاوية.

$\begin{aligned} \vec{L N} = ⟨ 1, 13, - 12 ⟩ \\ L N = | \vec{L N} | = \sqrt{1 + 169 + 144} = \sqrt{314} \\ \vec{M L} = ⟨ 7, - 4, 2 ⟩ \\ M L = | \vec{M L} | = \sqrt{49 + 16 + 4} = \sqrt{69} \\ \vec{N M} = ⟨ - 8, - 9, 10 ⟩ \\ N M = | \vec{N M} | = \sqrt{64 + 81 + 100} = \sqrt{245} \end{aligned}$

بما أن: $(L N)^{2} = (M L)^{2} + (N M)^{2}$ إذن: $314 = 69 + 245$

فإن $△ L M N$ قائم الزاوية في M (بعكس نظرية فيثاغورس).

(46) أجد مساحة المثلث LMN.

مساحة المثلث في A حيث:

$A = \frac{1}{2} (M L) (N M) = \frac{1}{2} \sqrt{69} \sqrt{245} = \frac{7}{2} \sqrt{345}$

إعداد : شبكة منهاجي التعليمية

14 / 02 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025