أتحقق من فهمي
الاقترانات اللوغاريتمية

(a) log2 16 = 4 → 24 = 16
(b) log7 7 = 1 → 71 = 7
(c) log3 () = -5 → 3-5 =
(d) log9 1 = 0 → 90 =

(a) 73 = 343 → log7 343 = 3
(b) = 7 → log49 7 =
(c) (2)-5 = → log2 = -5
(d) 170 = 1 → log17 1 = 0

(a)
log5 25 = y
5y = 25
5y = 52
y = 2
إذن: log5 25 = 2
(b)
Log8 = y
8y =
8y =
y =
إذن: log8 =
(c)
log81 9 = y
81y = 9
92y = 91
2y = 1
y =
إذن: log81 9 =
(d)
log3 = y
3y =
3y =
3y = 3-3
y = -3
إذن: log3 = -3

(a) log2 1 = 0
(b) log32 = log32 =
(c) log9 9 = 1
(d) 8log8 13 = 13

(a)
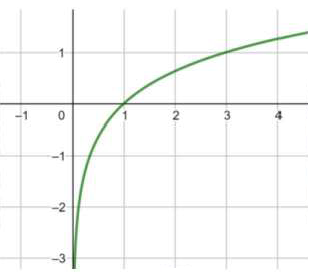
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحورy
الاقتران متزايد.
(b)
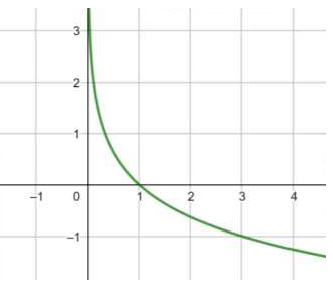
مجال هذا الاقتران هو مجموعة الأعداد الحقيقية الموجبة R+ أي (0 , ).
مدى هذا الاقتران هو مجموعة الأعداد الحقيقية R
المقطع x هو 1 ، ولا يوجد مقطع y
لهذا الاقتران خط تقارب رأسي هو المحورy
الاقتران متناقص.

(a)
5 – x > 5
-x > -5
x < 5
مجال الاقتران هو ( , 5-)
(b)
9 + 3x > 0
3x > -9
x > -3
مجال الاقتران هو (-3 , )
إعداد : شبكة منهاجي التعليمية
10 / 07 / 2023
النقاشات