مهارات التفكير العليا

الاقترانات اللوغاريتمية

تبرير: أكتب بجانب كل اقتران ممّا يأتي رمز تمثيله البياني المناسب، مبرراً إجابتي:

(38) f(x) = log₃ (x)

c

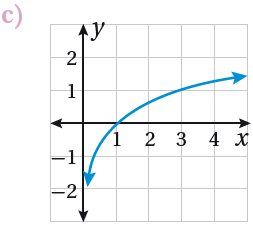
لأن مجال الاقتران هو (0 , )، وهو متزايد ويمر منحناه بالنقطة (3, 1) حيث:

f(3) = log₃ 3 = 1

(39) f(x) = log₃ (-x)

b

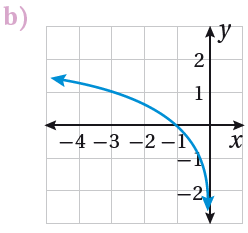
لأن مجال الاقتران هو ( , 0)، ويمر منحناه بالنقطة (-3, 1) حيث:

f(-3) = log₃ (-(-3)) = log₃ (3) = 1

(40) g(x) = -log₃ x

a

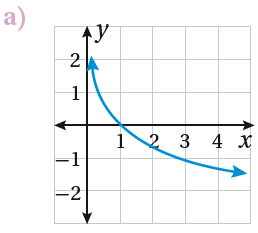
لأن مجال الاقتران هو (0 , )، وهو متناقص ويمر منحناه بالنقطة (3, -1) حيث:

f(3) = -log₃ 3 = -1

تحدّ: أجد مجال كل اقتران لوغاريتمي ممّا يأتي، محدداً خط (خطوط) تقاربه الرأسي:

(41) f(x) = log₃ (x²)

بما أن x² > 0 لجميع الأعداد الحقيقية عدا العدد 0

فإن مجال هذا الاقتران هو R – {0}

خط التقارب الرأسي هو x = 0 (المحور y ).

(42) f(x) = log₃ (x² – x - 2)

x² – x – 2 > 0

(x – 2) (x + 1) > 0

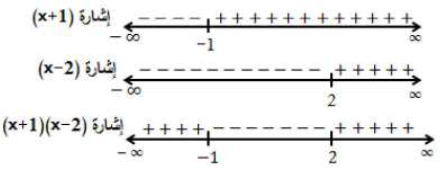
نلاحظ أن (x – 2) (x + 1) > 0 في الفترتين ( , -1) و (2, ).

إذن مجال الاقتران هو (2, )  ( , -1).

خطا التقارب الرأسيان هما x = -1 , x = 2 ،  وهما جذرا المعادلة: x² – x – 2 = 0

(43) f(x) = log₃ ()

يكون > 0  عندما يكون البسط والمقام موجبان معاً، أو سالبان معاً.

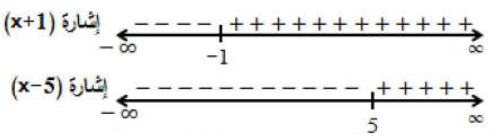
نلاحظ أنx –5 , x + 1   لهما الإشارة نفسها في الفترتين ( , -1) و (5, ).

إذن مجال الاقتران هو (5, )  ( , -1).

خطا التقارب الرأسيان هما x = -1 , x = 5 ،  وهما جذرا المعادلتين: x – 5 = 0 , x + 1 = 0

(44) أكتشف الخطأ: كتبت منى المعادلة الأسيّة: 4^-3 =  في صورة لوغاريتمية كما يأتي:

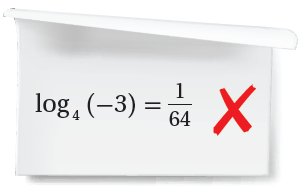
أكتشف الخطأ الذي وقعت فيه منى، ثم أصححه.

الكتابة الصحيحة للصورة اللوغاريتمية هي:

log₄  = -3