مهارات التفكير العليا

مهارات التفكير العليا

قوانين اللوغاريتمات

$مهارات التفكير العليا$

(26) تحدّ: أثبت أنّ: $\frac{3}{2}$ = $\frac{\log_{a} 216}{\log_{a} 36}$

$\frac{3}{2}$ = $\frac{3 l o g_{a} 6}{2 l o g_{a} 6}$ = $\frac{l o g_{a} 6^{3}}{l o g_{a} 6^{2}}$ = $\frac{l o g_{a} 216}{l o g_{a} 36}$

(27) أكتشف الخطأ في الحلّ الآتي، ثم أصححه.

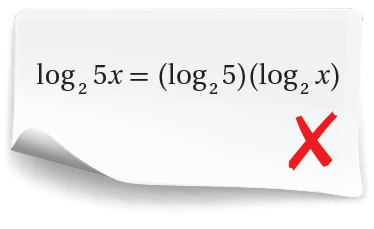
log₂ 5x = log₂ 5 + log₂ x

(18) تبرير: أثبت أنّ log_b (b - 3) + log_b (b² + 3b) – log_b (b² – 9) = 1 ، حيث b > 3 ، مبرراً إجابتي.

log_b (b - 3) + log_b (b² + 3b) – log_b (b² – 9)

log_b (b - 3) (b² + 3b) – log_b (b² – 9)

= log_b $\frac{(b - 3) (b^{2} + 3 b)}{(b^{2} - 9)}$

= 1

إعداد : شبكة منهاجي التعليمية

10 / 07 / 2023