مهارات التفكير العليا

نظرية فيثاغورس

18) أكتشف المختلف: أي المثلثات الآتية مختلف؟ أبرر إجابتي:

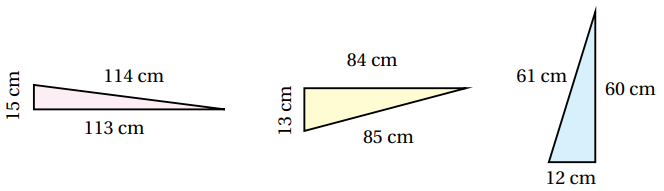
الأوسط هو المختلف لأنه قائم، أما المثلثان الآخران فليسا قائمين.

19) مسألة مفتوحة: ثلاثيات فيثاغورس هي مجموعات من ثلاثة أعداد موجبة a و b و c تحقق نظرية فيثاغورس؛ أي تشكل أطوالاً لمثلث قائم الزاوية. مثلاً: 3 و 4 و 5 . أجد مجموعتين من ثلاثيات فيثاغورس.

يوجد أكثر من إجابة منها (10 ,8 ,6) ، (13 ,12 ,5) .

20) تحد في الشكل الآتي، أجد طول PQ من دون استعمال المسطرة.

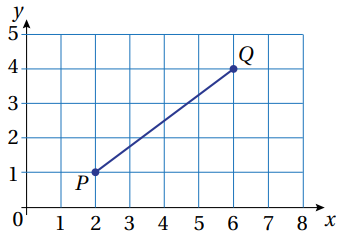
5

21) تبرير: أقارن بين مساحة نصف الدائرة الكبيرة ومساحة نصفي الدائرتين الصغيرتين، مبرراً إجابتي.

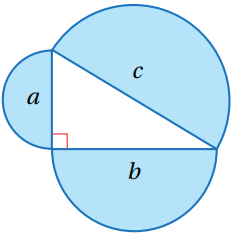
مساحة نصف الدائرة الصغرى التي قطرها a هو: a²

مساحة نصف الدائرة الصغرى التي قطرها b هو: b²

مساحة نصف الدائرة الكبرى التي قطرها b هو: c²

ومنه:+ b² = (a² + b²) = c²  a²

إذن، مساحة نصف الدائرة الكبرى يساوي مجموع مساحتي نصفي الدائرتين الصغيرتين.

22) أكتب كيف أجد طول ضلع مجهولاً في مثلث قائم الزاوية باستخدام نظرية فيثاغورس؟