أتدرب وأحل المسائل
مشتقتا الضرب والقسمة والمشتقات العليا
أجد مشتقة كل اقتران ممّا يأتي:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
إذا كان f(x) و g(x) اقترانين قابلين للاشتقاق عندما x = 0 ، وكان:
فأجد كلاً ممّا يأتي:
(12)
(13)
(14)
أجد المشتقة الثانية لكل اقتران ممّا يأتي عند قيمة x المعطاة:
(15)
(16)
(17)
أجد معادلة المماس لكل اقتران ممّا يأتي عند النقطة المعطاة:
(18)
ميل المماس عند النقطة (0, ) هو: f ’(0) =
معادلة المماس هي:
(19)
ميل المماس عند النقطة (0, 1) هو:
معادلة المماس هي:
أثبت صحّة كلّ ممّا يأتي معتمداً أنّ :
(20)
(21)
(22)
ألاحظ المشتقة المعطاة في كلّ ممّا يأتي، ثم أجد المشتقة العليا المطلوبة:
(23)
(24)
(25)
 (26) نباتات هجينة: وجد فريق بحث زراعي أنّه يمكن التعبير عن ارتفاع نبتة هجينة من نبات تبّاع الشمس h بالأمتار، باستعمال الاقتران: h(t) = ، حيث t الزمن بالأشهر بعد زراعة البذور. أجد معدّل تغير ارتفاع النبتة بالنسبة إلى الزمن.
(26) نباتات هجينة: وجد فريق بحث زراعي أنّه يمكن التعبير عن ارتفاع نبتة هجينة من نبات تبّاع الشمس h بالأمتار، باستعمال الاقتران: h(t) = ، حيث t الزمن بالأشهر بعد زراعة البذور. أجد معدّل تغير ارتفاع النبتة بالنسبة إلى الزمن.
إذا كان الاقتران: y = ex sin x ، فأجيب عن السؤالين الآتيين تباعاً:
(27) أجد ، و .
(28) أثبت أنّ
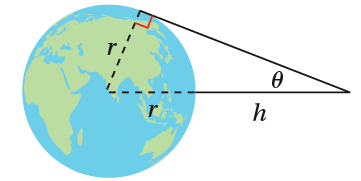 أقمار صناعية: عندما ترصد الأقمار الصناعية الأرض، فإنه يُمكنها مسح جزء فقط من سطح الأرض. وبعض الأقمار الصناعية تحوي مُستشعرات لقياس الزاوية Ɵ (بالراديان) المبينة في الشكل المجاور. إذا كان h يمثل المسافة بين القمر الصناعي وسطح الأرض بالكيلومترات، و r يُمثل نصف قطر الأرض بالكيلومترات، فأجيب عن السؤالين الآتيين تباعاً:
أقمار صناعية: عندما ترصد الأقمار الصناعية الأرض، فإنه يُمكنها مسح جزء فقط من سطح الأرض. وبعض الأقمار الصناعية تحوي مُستشعرات لقياس الزاوية Ɵ (بالراديان) المبينة في الشكل المجاور. إذا كان h يمثل المسافة بين القمر الصناعي وسطح الأرض بالكيلومترات، و r يُمثل نصف قطر الأرض بالكيلومترات، فأجيب عن السؤالين الآتيين تباعاً:
(29) أثبت أنّ h = r(csc Ɵ - 1) .
(30) أجد معدل تغير h بالنسبة إلى Ɵ عندما (أفترض أن r = 6371 km).
(31) إذا كان: ، فأثبت أنّ .
يبين الشكل المجاور منحنيي الاقتراني: F(x) ، و G(x) .
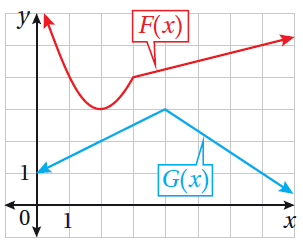
إذا كان: P(x) = F(x)G(x) ، وكان: Q(x) = ، فأجد كلاً ممّا يأتي:
(32) P’(2)
(2) G’ ميل المستقيم الذي يمر بالنقطتين (2, 2) و (4, 3) ويساوي
(2) F’ ميل المماس الأفقي، ويساوي صفراً.
(33) Q’(7)

 (26) نباتات هجينة: وجد فريق بحث زراعي أنّه يمكن التعبير عن ارتفاع نبتة هجينة من نبات تبّاع الشمس h بالأمتار، باستعمال الاقتران: h(t) = ، حيث t الزمن بالأشهر بعد زراعة البذور. أجد معدّل تغير ارتفاع النبتة بالنسبة إلى الزمن.
(26) نباتات هجينة: وجد فريق بحث زراعي أنّه يمكن التعبير عن ارتفاع نبتة هجينة من نبات تبّاع الشمس h بالأمتار، باستعمال الاقتران: h(t) = ، حيث t الزمن بالأشهر بعد زراعة البذور. أجد معدّل تغير ارتفاع النبتة بالنسبة إلى الزمن. أقمار صناعية: عندما ترصد الأقمار الصناعية الأرض، فإنه يُمكنها مسح جزء فقط من سطح الأرض. وبعض الأقمار الصناعية تحوي مُستشعرات لقياس الزاوية Ɵ (بالراديان) المبينة في الشكل المجاور. إذا كان h يمثل المسافة بين القمر الصناعي وسطح الأرض بالكيلومترات، و r يُمثل نصف قطر الأرض بالكيلومترات، فأجيب عن السؤالين الآتيين تباعاً:
أقمار صناعية: عندما ترصد الأقمار الصناعية الأرض، فإنه يُمكنها مسح جزء فقط من سطح الأرض. وبعض الأقمار الصناعية تحوي مُستشعرات لقياس الزاوية Ɵ (بالراديان) المبينة في الشكل المجاور. إذا كان h يمثل المسافة بين القمر الصناعي وسطح الأرض بالكيلومترات، و r يُمثل نصف قطر الأرض بالكيلومترات، فأجيب عن السؤالين الآتيين تباعاً: