أتحقق من فهمي

مشتقة اقترانات خاصة

الاتصال والاشتقاق

أتحقق من فهمي صفحة 10

يبين الشكل الآتي منحنى الاقتران f(x) . أحدّد قيم x للنقاط التي يكون عندها الاقتران f(x)  غير قابل للاشتقاق، مبرراً إجابتي.

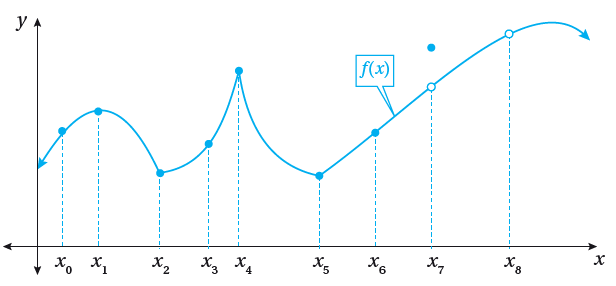
الاقتران f غير قابل للاشتقاق عندما:

x = x₂  ,  x = x₄  ,  x = x₅

لأن لمنحناه رأس حادّ أو زاوية عند هذه النقاط.

الاقتران f غير قابل للاشتقاق عندما:

x = x₇  ,  x = x₈

لأنه غير متصل عندهما.

مشتقة الاقتران الأسي الطبيعي

أتحقق من فهمي صفحة 12

أجد مشتقة كل اقتران ممّا يأتي:

(a) f(x) = 5e^x + 3

f(x) = 5e^x + 3

f ’(x) = 5e^x

(b) f(x) =  - 4e^x

f(x) =  - 4e^x =  - 4e^x

f ’(x) = - 4e^x =  - 4e^x

(c) y = 8e^x +

f(x) = 8e^x +  = 8e^x + 4

f ’(x) = 8e^x -  = 8e^x -

مشتقة الاقتران اللوغاريتمي الطبيعي

أتحقق من فهمي صفحة 14

أجد مشتقة كل اقتران ممّا يأتي:

(a) f(x) =  + ln (4x)

f(x) =  + ln (4x) =  + ln 4 + ln x

f ’(x) =  +  =  +

(b) f(x) = ln (2x³)

f(x) = ln (2x³) = ln 2 + 3 ln x

f ’(x) =

مشتقة اقتران الجيب، ومشتقة اقتران جيب التمام

أتحقق من فهمي صفحة 16

أجد مشتقة كل اقتران ممّا يأتي:

(a) y =  + 3 cos x

y =  + 3 cos x =  sin x + 3 cos x

  = cos x – 3 sin x

(b) f(x) = x² + cos x + sin

f(x) =  x² + cos x + sin

f ’(x) = 2x – sin x

تطبيقات: معادلة المماس والعمودي عند نقطة ما

أتحقق من فهمي صفحة 17

إذا كان الاقتران: f(x) = ln  ، فأستعمل المشتقة لإيجاد كلّ ممّا يأتي:

(a) معادلة المماس عند النقطة (e, ).

f(x) = ln  =  ln x    →    f ’(x) =

ميل المماس عند النقطة (e, ) هو:

f ’(e) = 

معادلة المماس عند النقطة (e, ) هي:

y -  =  (x – e)

y = x

(b) معادلة العمودي على المماس عند النقطة (e, ).

بما أن ميل المماس عند النقطة (e, ) هو  ، إذن ميل العمودي على المماس عندها هو e-2e 

معادلة العمودي على المماس عند النقطة (e, ) هي:

y - = -2e (x - e)

y =  -2ex + 2e² +

تطبيقات: الحركة في مسار مستقيم

أتحقق من فهمي صفحة 20

يمثل الاقتران: s(t) = t² – 7t + 8, t  0  موقع جسم يتحرك في مسار مستقيم، حيث s الموقع بالأمتار و t الزمن بالثواني:

(a) أجد سرعة الجسم المتجهة وتسارعه عندما t = 4 .

s(t) = t² – 7t + 8

v(t) = 2t – 7  →   v(4) = 1 m/s

a(t) = 2   →  a(4) = 2 m/s²

(b) أجد قيم t التي يكون عندها الجسم في حالة سكون لحظي.

v(t) = 2t – 7 = 0   →   t =  s

(c) في أيّ اتجاه يتحرك الجسم عندما t = 2 ؟

v(2) = -3 m/s

بما أن إشارة المتجهة سالبة، فإن الجسم يتحرك لليسار عندما t = 2

(d) متى يعود الجسم إلى موقعه الابتدائي؟

الموقع الابتدائي للجسم:

s(t) = 8   →   t² – 7t + 8 = 8   →   t² – 7t = 0

t(t – 7) = 0   →   t = 0  or  t = 7

إذن يعود الجسم إلى موقعه الابتدائي عندما  t = 7 s

تطبيقات: الحركة التوافقية البسيطة

أتحقق من فهمي صفحة 22

يتحرك جسم معلق بزنبرك إلى الأعلى وإلى الأسفل، ويمثل الاقتران:s(t) = 7 sin t  موقع الجسم عند أيّ زمن لاحق، حيث t الزمن بالثواني و s الموقع بالأمتار:

(a) أجد اقتراناً يمثل سرعة الجسم المتجهة، واقتراناً آخر يمثل تسارعه عند أيّ لحظة.

s(t) = 7 sin t

v(t) = 7 cos t

a(t) = -7 sin t

(b) أصف حركة الجسم.

بالنظر لاقتران الموقع s(t) فإن قيم s تنحصر بين 7 m وهذا يعني أن الجسم يتحرك بمرور الزمن صعوداً وهبوطاً بين الموقعين s = -7 m , s = 7 m ، ويمر بنقطة الاتزان s = 0 عند قيم t التي تحقق s(t) = 0 وهي t = ns حيث n أي عدد صحيح غير سالب.

تتغير سرعة الجسم بمرور الزمن وتتراوح بين القيمتين 7 m/s ويكون مقدار سرعة الجسم أكبر ما يمكن = 7 عندما cos t = 1 وذلك عندما t = n (نفسها لحظات مرور الجسم بنقطة الاتزان)، بينما تكون سرعة الجسم صفراً (يسكن لحظياً) عندما يكون الجسم في أقصى بعد له عن نقطة الاتزان → v(t) = 0   (اللحظات t =  حيث n عدد فردي موجب).

نلاحظ أن قيمة تسارع الجسم عند كل لحظة هي معكوس قيمة موقعه وأن التسارع ينعدم لحظة مرور الجسم بنقطة الاتزان، وهي اللحظة التي تكون محصلة القوى المؤثرة على الجسم فيها صفراً.