أتحقق من فهمي
التكامل بالأجزاء
التكامل بالأجزاء
أتحقق من فهمي صفحة (63):
أجد كلاً من التكاملات الآتية:
(a)
(b)
(c)
ملاحظة: يمكن حل هذه المسألة بطريقة التعويض
وتالياً حلها بالأجزاء:
(d)
تكرار التكامل بالأجزاء
أتحقق من فهمي صفحة (64):
أجد كلاً من التكاملين الآتيين:
(a)
(b)
التكاملات الدورية
أتحقق من فهمي صفحة (66):
أجد كلاً من التكاملين الآتيين:
(a)
(b)
تكرار التكامل بالأجزاء باستعمال طريقة الجدول
أتحقق من فهمي صفحة (67):
أجد كلاً من التكاملين الآتيين:
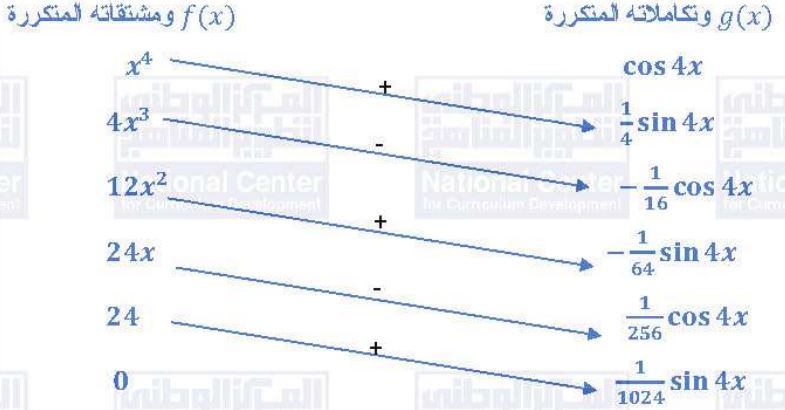
(a)
نفرض أن: ، استخدم طريقة الجدول للتكامل بالأجزاء:
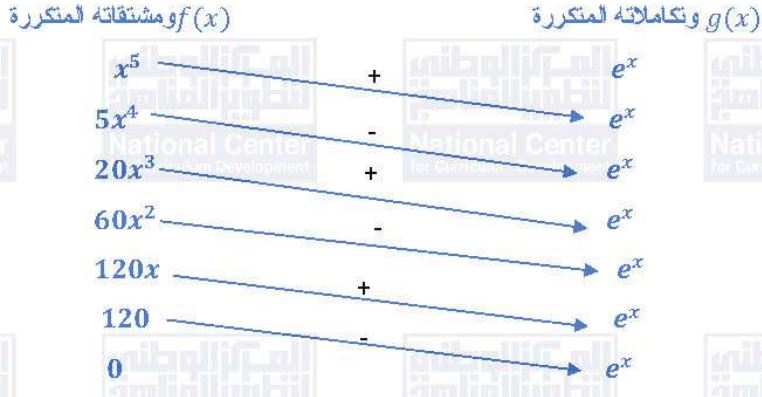
(b)
نفرض أن: ، استخدم طريقة الجدول للتكامل بالأجزاء:
أتحقق من فهمي صفحة (68):
التكلفة الحدية: يمثل الاقتران: التكلفة الحدية لكل قطعة (بالدينار) تنتج في إحدى الشركات، حيث عدد القطع المنتجة، و تكلفة إنتاج قطعة بالدينار. أجد اقتران التكلفة ، علماً بأن .
التكامل بالأجزاء لتكاملات محدودة
أتحقق من فهمي صفحة (70):
أجد كلاً من التكاملين الآتيين:
(a)
(b)
التكامل بالأجزاء، والتكامل بالتعويض
أتحقق من فهمي صفحة (71):
أجد قيمة كل من التكاملين الآتيين:
(a)
نجد كل تكامل على حدة. فنجد التكامل الأيسر كما يأتي:
ونجد التكامل الأيمن كما يأتي:
(b)


النقاشات