مهارات التفكير العليا

مهارات التفكير العليا

التكامل بالأجزاء

(37) تبرير: أثبت أن: $\int_{1 / 2}^{3} x^{2} \ln 2 x d x = 9 \ln 6 - \frac{215}{72}$ .

$\begin{aligned} u = \ln 2 x d v = x^{2} d x \\ d u = \frac{1}{x} d x v = \frac{1}{3} x^{3} \\ \int_{\frac{1}{2}}^{3} x^{2} \ln 2 x d x = {\frac{1}{3} x^{3} \ln 2 x |}_{\frac{1}{2}}^{3} - \int_{\frac{1}{2}}^{3} \frac{1}{3} x^{2} d x \\ = {\frac{1}{3} x^{3} \ln 2 x |}_{\frac{1}{2}}^{3} - {\frac{1}{9} x^{3} |}_{\frac{1}{2}}^{3} \\ = 9 \ln 6 - 3 + \frac{1}{72} = 9 \ln 6 - \frac{215}{72} \end{aligned}$

(38) تبرير: أثبت أن: $\int_{0}^{π / 4} x \sin 5 x \sin 3 x d x = \frac{π - 2}{16}$ .

$\begin{aligned} u = x d v = \sin 5 x \sin 3 x d x = \frac{1}{2} (\cos 2 x - \cos 8 x) d x \\ d u = d x v = \frac{1}{4} \sin 2 x - \frac{1}{16} \sin 8 x \\ \int_{0}^{\frac{π}{4}} x \sin 5 x \sin 3 x d x \\ = {x (\frac{1}{4} \sin 2 x - \frac{1}{16} \sin 8 x) |}_{0}^{\frac{π}{4}} - \int_{0}^{\frac{π}{4}} (\frac{1}{4} \sin 2 x - \frac{1}{16} \sin 8 x) d x \\ = {x (\frac{1}{4} \sin 2 x - \frac{1}{16} \sin 8 x) |}_{0}^{\frac{π}{4}} - {(- \frac{1}{8} \cos 2 x + \frac{1}{128} \cos 8 x) |}_{0}^{\frac{π}{4}} \\ = \frac{π}{4} (\frac{1}{4}) + 0 - \frac{1}{128} - \frac{1}{8} + \frac{1}{128} = \frac{π - 2}{16} \end{aligned}$

(39) تبرير: إذا كان: $\int_{0}^{a} x e^{x / 2} d x = 6$ ، فأثبت أن $a$ يحقق المعادلة: $x = 2 + e^{- x / 2}$ .

$\begin{aligned} u = x d v = e^{\frac{1}{{\bar{2}}^{x}}} d x \\ d u = d x v = 2 e^{\frac{1}{2^{x}}} \\ \int_{0}^{a} x e^{\frac{1}{2^{2}} x} d x = {2 x e^{\frac{1}{2^{2}}} |}_{0}^{a} - \int_{0}^{a} 2 e^{\frac{1}{2} x} d x \\ = {2 x e^{\frac{1}{2} x} |}_{0}^{a} - {4 e^{\frac{1}{2} x} |}_{0}^{a} \\ = 2 a e^{\frac{1}{z^{a}}} - 4 e^{\frac{1}{2^{a}}} + 4 \\ \Rightarrow 2 a e^{\frac{1}{2^{a}}} - 4 e^{\frac{1}{2^{a}}} + 4 = 6 \\ 2 α e^{\frac{1}{{\bar{2}}^{a}}} = 4 e^{\frac{1}{{\bar{2}}^{a}}} + 2 \end{aligned}$

بقسمة طرفي المعادلة على $2 e^{\frac{1}{2} a}$ نحصل على:

$a = 2 + e^{- \frac{1}{2} a}$

لذا فإن $a$ يحقق المعادلة $x = 2 + e^{- \frac{x}{2}}$

(40) تبرير: أجد: $\int (\ln x)^{2} d x$ بطريقتين مختلفتين، مبرراً إجابتي.

الطريقة الأولى بالتعويض:

$\begin{aligned} u = \ln x \Rightarrow \frac{d u}{d x} = \frac{1}{x} \Rightarrow d x = x d u, x = e^{u} \\ \int (\ln x)^{2} d x = \int u^{2} x d u = \int u^{2} e^{u} d u \end{aligned}$

بالأجزاء مرتين، نستخدم الجدول:

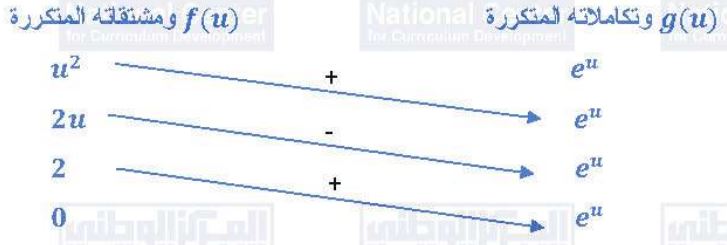
حل السؤال 40

$\begin{aligned} \int u^{2} e^{u} d u = e^{u} (u^{2} - 2 u + 2) + C \\ \int (\ln x)^{2} d x = e^{\ln x} ((\ln x)^{2} - 2 \ln x + 2) + C \\ = x ((\ln x)^{2} - 2 \ln x + 2) + C \end{aligned}$

الطريقة الثانية: بالأجزاء مباشرة:

$\begin{aligned} u = (l n x)^{2} d v = d x \\ d u = \frac{2 l n x}{x} d x v = x \\ \int (l n x)^{2} d x = x (l n x)^{2} - \int 2 l n x d x \end{aligned} \begin{aligned} u = 2 l n x d v = d x \\ d u = \frac{2}{x} d x v = x \\ \int (l n x)^{2} d x = x (l n x)^{2} - 2 x l n x + \int 2 d x \\ = x (l n x)^{2} - 2 x l n x + 2 x + C \end{aligned}$

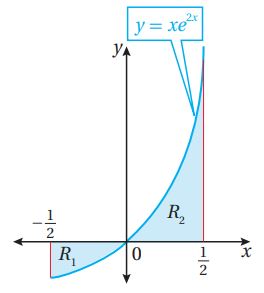تبرير: إذا كان الشكل المجاور يمثل منحنى الاقتران: $y = x e^{2 x}$ حيث: $- \frac{1}{2} \leq x \leq \frac{1}{2}$ ، فأجيب عن السؤالين الآتيين تباعاً:

(41) أجد مساحة كل من المنطقة $R_{1}$ ، والمنطقة $R_{2}$ .

$A_{1} = - \int_{- \frac{1}{2}}^{0} x e^{2 x} d x, A_{2} = \int_{0}^{\frac{1}{2}} x e^{2 x} d x$

نجد التكامل غير المحدود $\int x e^{2 x} d x$ بالأجزاء:

$\begin{aligned} u & = x & d v & = e^{2 x} d x \\ d u & = d x & v & = \frac{1}{2} e^{2 x} \end{aligned} \begin{aligned} \int \begin{aligned} \int x e^{2 x} d x = \frac{1}{2} x e^{2 x} - \int \frac{1}{2} e^{2 x} d x \\ = \frac{1}{2} x e^{2 x} - \frac{1}{4} e^{2 x} + C \\ = \frac{1}{4} e^{2 x} (2 x - 1) + C \\ \Rightarrow A (R_{1}) = - {\frac{1}{4} e^{2 x} (2 x - 1) |}_{\frac{1}{2}}^{0} = \frac{1}{4} - \frac{1}{2 e} = \frac{e - 2}{4 e} \\ A (R_{2}) = {\frac{1}{4} e^{2 x} (2 x - 1) |}_{0}^{\frac{1}{2}} = 0 + \frac{1}{4} = \frac{1}{4} \end{aligned} \end{aligned}$

(42) أثبت أن مساحة المنطقة $R_{1}$ إلى مساحة المنطقة $R_{2}$ تساوي $(e - 2) : e$ .

$\begin{aligned} \frac{A (R_{1})}{A (R_{2})} = \frac{\frac{e - 2}{4 e}}{\frac{1}{4}} = \frac{e - 2}{e} \\ A (R_{1}) : A (R_{12}) = (e - 2) : e \end{aligned}$

تحد: استعمل التكامل بالأجزاء لإثبات كل مما يأتي، حيث: $n$ عدد صحيح موجب، و $a \neq 0$ :

$\int x^{n} \ln x d x = \frac{x^{n + 1}}{(n + 1)^{2}} (- 1 + (n + 1) \ln x) + C$ (43)

$\begin{aligned} u = \ln x d v = x^{n} d x \\ d u = \frac{1}{x} d x v = \frac{1}{n + 1} x^{n + 1} \\ \int x^{n} \ln x d x = \frac{x^{n + 1} \ln x}{n + 1} - \int \frac{1}{n + 1} x^{n} d x \\ = \frac{x^{n + 1} \ln x}{n + 1} - \frac{1}{(n + 1)^{2}} x^{n + 1} + C \\ = \frac{x^{n + 1}}{(n + 1)^{2}} (- 1 + (n + 1) \ln x) + C \end{aligned}$

$\int x^{n} e^{a x} d x = \frac{x^{n} e^{a x}}{a} - \frac{n}{a} \int x^{n - 1} e^{a x} d x$ (44)

$\begin{aligned} u = x^{n} d v = e^{a x} d x \\ d u = n x^{n - 1} d x v = \frac{1}{a} e^{a x} \\ \int x^{n} e^{a x} d x = \frac{1}{a} x^{n} e^{a x} - \frac{n}{a} \int x^{n - 1} e^{a x} d x \end{aligned}$

إعداد : شبكة منهاجي التعليمية

12 / 02 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025