أتدرب وأحل المسائل - 1

أتدرب وأحل المسائل

الأسئلة (1 - 20)

الاشتقاق

أبحث قابلية اشتقاق كل اقتران ممّا يأتي عند قيمة x المعطاة:

(1) $f (x) = | x - 5 |, x = 5$

$\begin{aligned} f^{'} (5) & = lim_{h \to 0} \frac{f (5 + h) - f (5)}{h} \\ = lim_{h \to 0} \frac{| (5 + h) - 5 | - 0}{h} \\ = lim_{h \to 0} \frac{| h |}{h} \\ f_{+}^{'} (5) & = lim_{h \to 0^{+}} \frac{h}{h} = 1 \\ f_{-}^{'} (5) & = lim_{h \to 0^{-}} \frac{- h}{h} = - 1 \end{aligned}$

بما أن النهايتين من اليمين واليسار غير متساويتين، فإن f '(5) غير موجودة، أي أنّ f غير قابل للاشتقاق عند x = 5

(2) $f (x) = x^{2 / 5}, x = 0$

$\begin{aligned} f^{'} (0) & = lim_{h \to 0} \frac{f (0 + h) - f (0)}{h} \\ = lim_{h \to 0} \frac{(h)^{\frac{2}{5}} - 0}{h} \\ = lim_{h \to 0} \frac{h^{\frac{2}{5}}}{h} = lim_{h \to 0} \frac{1}{h^{\frac{3}{5}}} \\ f_{+}^{'} (0) & = \infty \\ f_{-}^{'} (0) & = - \infty \end{aligned}$

f ‘(0) غير موجودة، إذن f غير قابل للاشتقاق عند x = 0

(3) $f (x) = {\begin{cases} x^{2} & , x \leq 1 \\ x^{2} - 2 x & , x > 1 \end{cases}, x = 1$

$\begin{aligned} f_{+}^{'} (1) & = lim_{h \to 0} \frac{f (1 + h) - f (1)}{h} \\ = lim_{h \to 0} \frac{(1 + h)^{2} - 2 (1 + h) - 1}{h} \\ = lim_{h \to 0} \frac{1 + 2 h + h^{2} - 2 - 2 h - 1}{h} = lim_{h \to 0} \frac{h^{2} - 2}{h} = - \infty \end{aligned}$

$f_{+}^{'} (1)$ غير موجودة، إذن f غير قابل للاشتقاق عند x = 1

(4) $f (x) = \frac{3}{x}, x = 4$

$\begin{aligned} f^{'} (4) & = lim_{h \to 0} \frac{f (4 + h) - f (4)}{h} \\ = lim_{h \to 0} \frac{\frac{3 + h}{4 + \frac{3}{4}}}{h} \\ = lim_{h \to 0} \frac{12 - 12 - 3 h}{4 h (4 + h)} = lim_{h \to 0} \frac{- 3}{4 (4 + h)} = \frac{- 3}{16} \end{aligned}$

f ‘(4) غير موجودة، إذن f قابل للاشتقاق عند x = 4

(5) $f (x) = (x - 6)^{2 / 3}, x = 6$

$\begin{aligned} f^{'} (6) & = lim_{h \to 0} \frac{f (6 + h) - f (6)}{h} \\ = lim_{h \to 0} \frac{(6 + h - 6)^{\frac{2}{3}} - 0}{h} \\ = lim_{h \to 0} \frac{(h)^{\frac{2}{3}}}{h} = lim_{h \to 0} \frac{1}{h^{\frac{1}{3}}} \\ f_{+}^{'} (6) & = \infty \\ f_{-}^{'} (6) & = - \infty \end{aligned}$

f ‘(6) غير موجودة، إذن f غير قابل للاشتقاق عند x = 6

(6) $f (x) = {\begin{cases} x + 1 & , x \neq 4 \\ 3 & , x = 4 \end{cases}, x = 4$

$\begin{aligned} f^{'} (4) & = lim_{h \to 0} \frac{f (4 + h) - f (4)}{h} \\ = lim_{h \to 0} \frac{4 + h + 1 - 3}{h} \\ = lim_{h \to 0} \frac{h + 2}{h} \\ f_{+}^{'} (4) & = \infty \\ f_{-}^{'} (4) & = - \infty \end{aligned}$

f ‘(4) غير موجودة، إذن f غير قابل للاشتقاق عند x = 4

أحدد قيم x للنقاط التي لا يكون عندها كلّ اقتران ممّا يأتي قابلاً للاشتقاق، مبرراً إجابتي:

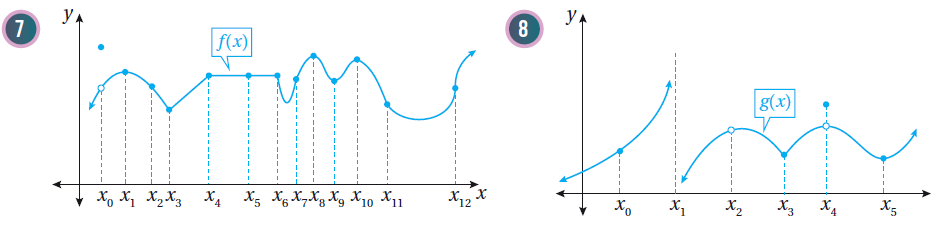
(7) الاقتران f غير قابل للاشتقاق عندما x = x₃, x = x₄, x = x₆ ؛ لأن لمنحناه رأس حاد أو زاوية عند هذه النقاط.

وهو غير قابل للاشتقاق عندما x = x₀ ؛ لأنه غير متصل عندها،

وهو غير قابل للاشتقاق عندما x = x₁₂ ؛ نظراً لوجود مماس رأسي عند هذه النقطة.

(8) الاقتران g غير قابل للاشتقاق عندماx = x₃ ؛ لأن لمنحناه زاوية عند هذه النقطة.

وهو غير قابل للاشتقاق عندما x = x₀ ؛ لأنه غير متصل عندها،

وهو غير قابل للاشتقاق عندما x = x₁, x = x₂, x = x₄ ؛ لأنه غير متصل عندها.

أحدد قيمة (قيم) x التي لا يكون عندها كلّ اقتران ممّا يأتي قابلاً للاشتقاق:

(9) $f (x) = \frac{x - 8}{x^{2} - 4 x - 5}$

f اقتران نسبي منحناه متصل وأملس عند جميع نقاطه باستثناء أصفار مقامه،

$x^{2} - 4 x - 5 = 0 \to (x - 5) (x + 1) = 0 \to x = 5 or x = - 1$

f غير متصل عند x = 5 , x = -1 إذن غير قابل للاشتقاق عندها.

(10) $f (x) = \sqrt[3]{3 x - 6} + 5$

$\begin{aligned} f (x) = \sqrt[3]{3 x - 6} \\ f^{'} (x) = \frac{1}{3} (3 x - 6)^{- \frac{2}{3}} (3) = \frac{1}{(3 x - 6)^{\frac{2}{3}}} \end{aligned}$

f ‘ (x) موجودة عند جميع قيم x الحقيقية عدا أصفار مقامها، إذن f غير قابل للاشتقاق عند x = 2

(11) $f (x) = | x^{2} - 9 |$

$f (x) = | x^{2} - 9 | = {\begin{matrix} 9 - x^{2}, - 3 < x < 3 \\ x^{2} - 9, x \leq - 3 or x \geq 3 \end{matrix}$

نبحث قابلية الاشتقاق عند x = 3 و x = -3 :

$\begin{aligned} f^{'} (3) & = lim_{h \to 0} \frac{f (3 + h) - f (3)}{h} \\ = lim_{h \to 0} \frac{| (3 + h)^{2} - 9 | - 0}{h} \\ = lim_{h \to 0} \frac{| 6 h + h^{2} |}{h} \\ f_{+}^{'} (3) & = lim_{h \to 0^{+}} \frac{6 h + h^{2}}{h} = lim_{h \to 0^{+}} (6 + h) = 6 \\ f_{-}^{'} (3) & = lim_{h \to 0^{-}} \frac{- 6 h - h^{2}}{h} = lim_{h \to 0^{-}} (- 6 - h) = - 6 \end{aligned}$

بما أن النهايتين من اليمين واليسار غير متساويتين فإن $f^{'} (3)$ غير موجودة أي أن f غير قابل للاشتقاق عند x = 3

$\begin{aligned} f^{'} (- 3) = lim_{h \to 0} \frac{f (- 3 + h) - f (- 3)}{h} \\ = lim_{h \to 0} \frac{| (- 3 + h)^{2} - 9 | - 0}{h} \\ = lim_{h \to 0} \frac{| 6 h - h^{2} |}{h} \\ f_{+}^{'} (- 3) = lim_{h \to 0^{+}} \frac{6 h - h^{2}}{h} = lim_{h \to 0^{+}} (6 - h) = 6 \\ f_{-}^{'} (- 3) = lim_{h \to 0^{-}} \frac{- 6 h + h^{2}}{h} = lim_{h \to 0^{-}} (- 6 + h) = - 6 \end{aligned}$

بما أن النهايتين من اليمين واليسار غير متساويتين فإن $f^{'} (- 3)$ غير موجودة أي أن f غير قابل للاشتقاق عند x = -3

إذن f غير قابل للاشتقاق عند x = 3 , x = -3

(12) إذا كان: $f (x) = x | x |$ ، فأثبت أنّ $f^{'} (0)$ موجودة.

$\begin{aligned} f (x) = x | x | \\ f^{'} (0) = lim_{h \to 0} \frac{f (0 + h) - f (0)}{h} \\ = lim_{h \to 0} \frac{h | h | - 0}{h} \\ = lim_{h \to 0} | h | \\ | h | = {\begin{array}{c} - h, h < 0 \\ h, h \geq 0 \end{array} \\ f_{+}^{'} (0) = lim_{h \to 0} h = 0 \\ f_{-}^{'} (0) = lim_{h \to 0} (- h) = 0 \end{aligned}$

بما أن النهايتين من اليمين واليسار متساويتان، إذن $f^{'} (0)$ موجودة.

أجد مشتقة كل اقتران ممّا يأتي:

(13) $f (x) = 2 \sin x - e^{x}$

$f^{'} (x) = 2 c o s x - e^{x}$

(14) $f (x) = \frac{\ln x}{4} - π \cos x$

$f^{'} (x) = \frac{1}{4 x} + π s i n x$

(15) $f (x) = \ln (\frac{1}{x^{3}}) + x^{4}$

$\begin{aligned} f (x) & = l n (\frac{1}{x^{3}}) + x^{4} \\ = l n 1 - l n x^{3} + x^{4} \\ = - 3 l n x + x^{4} \\ f^{'} (x) & = - \frac{3}{x} + 4 x^{3} \end{aligned}$

(16) $f (x) = e^{x + 1} + 1$

$\begin{aligned} f (x) = e^{x + 1} + 1 = e \times e^{x} + 1 \\ f^{'} (x) = e \times e^{x} = e^{x + 1} \end{aligned}$

(17) $f (x) = e^{x} + x^{e}$

$f^{'} (x) = e^{x} + e x^{e - 1}$

(18) $f (x) = \ln (\frac{10}{x^{n}})$

$\begin{aligned} f (x) & = l n (\frac{10}{x^{n}}) \\ = l n 10 - l n x^{n} = l n 10 - n l n x \\ f^{'} (x) & = - n (\frac{1}{x}) = - \frac{n}{x} \end{aligned}$

إذا كان: $f (x) = s i n x + \frac{1}{2} e^{x}$ ، فأجيب عن السؤالين الآتيين تباعاً:

(19) أجد معادلة المماس لمنحنى الاقتران f عند النقطة ( $π, \frac{1}{2} e^{π}$ ).

$f^{'} (x) = c o s x + \frac{1}{2} e^{x}$

ميل المماس عند النقطة ( $π, \frac{1}{2} e^{π}$ ) :

$f^{'} (π) = c o s π + \frac{1}{2} e^{π} = - 1 + \frac{1}{2} e^{π}$

معادلة المماس عند النقطة ( $π, \frac{1}{2} e^{π}$ ) :

$\begin{aligned} y - \frac{1}{2} e^{π} = (- 1 + \frac{1}{2} e^{π}) (x - π) \\ y = (- 1 + \frac{1}{2} e^{π}) x + π - \frac{π}{2} e^{π} + \frac{1}{2} e^{π} \end{aligned}$

(20) أجد معادلة العمودي على المماس لمنحنى الاقتران f عند النقطة ( $π, \frac{1}{2} e^{π}$ ).

بما أن ميل المماس عند النقطة ( $π, \frac{1}{2} e^{π}$ ) هو $- 1 + \frac{1}{2} e^{π}$ ، فإن ميل العمودي على المماس هو:

$\frac{- 1}{- 1 + \frac{1}{2} e^{π}} = \frac{- 2}{- 2 + e^{π}} = \frac{2}{2 - e^{π}}$

معادلة العمودي على المماس هي:

$y - \frac{1}{2} e^{π} = \frac{2}{2 - e^{π}} (x - π) \to y = \frac{2}{2 - e^{π}} x - \frac{2 π}{2 - e^{π}} + \frac{1}{2} e^{π}$

إعداد : شبكة منهاجي التعليمية

10 / 07 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025