الشرط الأولي، وحدة التكامل التوجيهي الأدبي

أتدرب وأحل المسائل

أتدرب وأحل المسائل

الشرط الأولي

في كل مما يأتي المشتقة الأولى للاقتران f(x) ، ونقطة يمر بها منحنى y = f(x) . أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران f(x) :

(1) f(x) = x⁷

$\begin{aligned} f (x) = \int (x - 3) d x \\ = \frac{1}{2} x^{2} - 3 x + C \\ 9 = \frac{1}{2} \times (2)^{2} - 3 (2) + C \\ C = 13 \\ f (x) = \frac{1}{2} x^{2} - 3 x + 13 \end{aligned}$

(2) $f^{'} (x) = x^{2} - 4; (0, 7)$

$\begin{aligned} f (x) = \int (x^{2} - 4) d x \\ = \frac{1}{3} x^{3} - 4 x + C \\ 7 = \frac{1}{3} \times (0)^{3} - 4 (0) + C \\ C = 7 \\ f (x) = \frac{1}{3} x^{3} - 4 x + 7 \end{aligned}$

(3) $f^{'} (x) = 6 x^{2} - 4 x + 2; (1, 9)$

$\begin{aligned} f (x) = \int (6 x^{2} - 4 x + 2) d x \\ = 2 x^{3} - 2 x^{2} + 2 x + C \\ 9 = 2 (1)^{3} - 2 (1)^{2} + 2 (1) + C \\ C = 7 \\ f (x) = 2 x^{3} - 2 x^{2} + 2 x + 7 \end{aligned}$

(4) $f^{'} (x) = \sqrt{x} + \frac{1}{4} x^{2}; (4, 11)$

$\begin{aligned} f (x) & = \int (\sqrt{x} + \frac{1}{4} x^{2}) d x \\ = \int (x^{\frac{1}{2}} + \frac{1}{4} x^{2}) d x \\ = \frac{2}{3} x^{\frac{3}{2}} - \frac{1}{12} x^{3} + C \\ 11 = & \frac{2}{3} (4)^{\frac{3}{2}} - \frac{1}{12} (4)^{3} + C \\ C = & 11 \\ f (x) & = \frac{2}{3} x^{\frac{3}{2}} - \frac{1}{12} x^{3} + 11 \\ = \frac{2}{3} \sqrt{x^{3}} - \frac{1}{12} x^{3} + 11 \end{aligned}$

(5) $f^{'} (x) = (x + 2)^{2}; (1, 7)$

$\begin{aligned} f (x) = \int (x + 2)^{2} d x \\ = \int (x^{2} + 4 x + 4) d x \\ = \frac{1}{3} x^{3} + 2 x^{2} + 4 x + C \\ 7 = \frac{1}{3} (1)^{3} + 2 (1)^{2} + 4 (1) + C \\ C = \frac{2}{3} \\ f (x) = \frac{1}{3} x^{3} + 2 x^{2} + 4 x + \frac{2}{3} \end{aligned}$

(6) $f^{'} (x) = \frac{3}{\sqrt{x}} - x; (4, 0)$

$\begin{aligned} f (x) & = \int (\frac{3}{\sqrt{x}} - x) d x \\ = \int (3 x^{- \frac{1}{2}} - x) d x \\ = 6 x^{\frac{1}{2}} - \frac{1}{2} x^{2} + C \\ = 6 \sqrt{x} - \frac{1}{2} x^{2} \\ 0 = & 6 \sqrt{4} - \frac{1}{2} (4)^{2} + C \\ C = & - 4 \\ f (x) & = 6 \sqrt{x} - \frac{1}{2} x^{2} - 4 \end{aligned}$

(7) إذا كان ميل المماس لمنحنى العلاقة y هو: $\frac{d y}{d x} = 0.4 x + 3$ ، فأجد قاعدة العلاقة y ، علماً بأنّ منحناها يمر بالنقطة (0, 5).

$\begin{aligned} y = \int (0 .4 x + 3) d x \\ = 0 .2 x^{2} + 3 x + C \\ 5 = 0.2 (0)^{2} + 3 (0) + C \\ C = 5 \\ y = 0 .2 x^{2} + 3 x + 5 \end{aligned}$

(8) إذا كان ميل المماس لمنحنى الاقتران f(x) هو: $f^{'} (x) = \frac{x^{2} + 10}{x^{2}}$ ، فأجد قاعدة الاقتران f(x)، علماً بأنّ منحناها يمر بالنقطة (5, 2).

$\begin{aligned} f (x) & = \int \frac{x^{2} + 10}{x^{2}} d x \\ = \int (\frac{x^{2}}{x^{2}} + \frac{10}{x^{2}}) d x \\ = \int (1 + 10 x^{- 2}) d x \\ = x - 10 x^{- 1} + C \\ = x - \frac{10}{x} + C \\ 2 = & 5 - \frac{10}{5} + C \\ C = & - 1 \\ f (x) & = x - \frac{10}{x} - 1 \end{aligned}$

(9) يبين الشكل المجاور منحنى الاقتران f(x)، حيث: $f^{'} (x) = 3 x^{2} - 3$ .

أجد قاعدة الاقتران f(x).

$منحنى الاقتران f(x)$

$\begin{aligned} f (x) & = \int (3 x^{2} - 3) d x \\ = x^{3} - 3 x + C \end{aligned}$

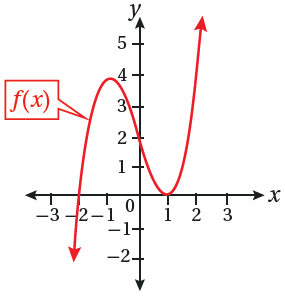
منحنى الاقتران يمر بالنقطة (0, 2)، إذن:

$\begin{aligned} 2 = (0)^{3} - 3 (0) + C \\ C = 2 \\ f (x) = x^{3} - 3 x + 2 \end{aligned}$

بالون: عند نفخ بالون كروي الشكل يصبح نصف قطره y سنتمتراً بعد t ثانية.

إذا كان: $\frac{d y}{d t} = 4 t^{- \frac{2}{3}}, t > 0$ ، وكان نصف قطر البالون بعد 8 ثوانٍ من بدء نفخه 30 cm ، فأجد كلاً مما يأتي:

(10) قاعدة العلاقة y بدلالة t .

$\begin{aligned} y = \int 4 t^{- \frac{2}{3}} d t \\ = 12 t^{\frac{1}{3}} + C \\ = 12 \sqrt[3]{t} + C \\ 30 = 12 \sqrt[3]{8} + C \\ C = 6 \\ y = 12 \sqrt[3]{t} + 6 \end{aligned}$

(11) نصف قطر البالون بعد 27 ثانية من بدء نفخه.

$\begin{aligned} y & = 12 \sqrt[3]{27} + 6 \\ = 42 \end{aligned}$

إذن نصف قطر البالون بعد 27ثانية من بدء نفخه هو: 42 cm

(12) أشجار: في دراسة تناولت نوعاً معيناً من الأشجار تبين أن ارتفاع هذه الأشجار يتغير بمعدل يمكن نمذجته بالاقتران: $h^{'} (t) = 0.2 t^{\frac{2}{3}} + \sqrt{t}$ ، حيث h(t) ارتفاع الشجرة بالأقدام، و t عدد السنوات منذ لحظة زراعة الشجرة. إذا كان ارتفاع إحدى هذه الأشجار عند زراعتها هو 2 ft فأجد h(t) .

$\begin{aligned} h (t) & = \int (0.2 t^{\frac{2}{3}} + \sqrt{t}) d t \\ = \int (0.2 t^{\frac{2}{3}} + t^{\frac{1}{2}}) d t \\ = 0.12 t^{\frac{5}{3}} + \frac{2}{3} t^{\frac{3}{2}} + C \\ = 0.12 \sqrt[3]{t^{5}} + \frac{2}{3} \sqrt{t^{3}} + C \end{aligned}$

بما أن ارتفاع الشجرة عند زراعتها 2 ft ، فإن h(0) = 2 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C .

$\begin{aligned} 2 = 0.12 \sqrt[3]{(0)^{5}} + \frac{2}{3} \sqrt{(0)^{3}} + C \\ C = 2 \\ h (t) = 0.12 \sqrt[3]{t^{5}} + \frac{2}{3} \sqrt{t^{3}} + 2 \end{aligned}$

(13) يتحرك جُسيم في مسار مستقيم، وتعطى سرعته المتجهة بالاقتران: v(t) = 2t + 3 ، حيث t الزمن بالثواني، و v سرعته المتجهة بالمتر لكل ثانية. إذا بدأ الجُسيم حركته من نقطة الأصل فأجد موقعه بعد 3 ثوانٍ من بدء الحركة.

$\begin{aligned} s (t) & = \int v (t) d t \\ = \int (2 t + 3) d t \\ = t^{2} + 3 t + C \end{aligned}$

بما أن الجُسيم بدأ حركته من نقطة الأصل، فإن s(0) = 0 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C .

$\begin{aligned} s (t) = t^{2} + 3 t + C \\ 0 = (0)^{2} + 3 (0) + C \\ C = 0 \\ s (t) = t^{2} + 3 t \\ s (3) = (3)^{2} + 3 (3) \\ = 18 \end{aligned}$

إذن موقع الجُسيم بعد 3 ثوان من بدء الحركة هو: 18 m

(14) يتحرك جُسيم في مسار مستقيم، ويعطى تسارعه بالاقتران: a(t) = t² ، حيث t الزمن بالثواني، و a تسارعه بالمتر لكل ثانية تربيع. إذا كان الموقع الابتدائي للجسيم هو 3 m، وكانت سرعته المتجهة هي 1 m/s بعد ثانية واحدة من بدء حركته، فأجد موقع الجسيم بعد ثانيتين من بدء الحركة.

$\begin{aligned} v (t) & = \int a (t) d t \\ = \int t^{2} d t \\ = \frac{1}{2} t^{3} + C_{1} \end{aligned}$

بما أن السرعة المتجهة بعد ثانية واحدة من بدء الحركة هي 1 m/s ، فإن v(1) = 1 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C₁ .

$\begin{aligned} 1 & = \frac{1}{2} (1)^{3} + C_{1} \\ C_{1} & = \frac{1}{2} \\ v (t) & = \frac{1}{2} t^{3} + \frac{1}{2} \\ s (t) & = \int v (t) d t \\ = \int (\frac{1}{2} t^{3} + \frac{1}{2}) d t \\ = \frac{1}{8} t^{4} + \frac{1}{2} t + C_{2} \end{aligned}$

بما أن الموقع الابتدائي للجُسيم هو 3 m ، فإن s(0) = 3 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C₂ .

$\begin{aligned} s (t) = \frac{1}{8} t^{4} + \frac{1}{2} t + C_{2} \\ 3 = \frac{1}{8} (0)^{4} + \frac{1}{2} (0) + C_{2} \\ C_{2} = 3 \\ s (t) = \frac{1}{8} t^{4} + \frac{1}{2} t + 3 \\ s (2) = \frac{1}{8} (2)^{4} + \frac{1}{2} (2) + 3 \\ = 5 \end{aligned}$

إذن موقع الجُسيم بعد ثانيتين من بدء الحركة هو: 5 m

(15) يتحرك جُسيم من السكون، ويعطى تسارعه بالاقتران: a(t) = 9 – 2t ، حيث t الزمن بالثواني، و a تسارعه بالمتر لكل ثانية تربيع. إذا بدأ الجسيم حركته من نقطة الأصل بسرعة متجهة هي 2 m/s ، فأجد موقعه بعد ثانيتين من بدء الحركة.

$\begin{aligned} v (t) & = \int a (t) d t \\ = \int (9 - 2 t) d t \\ = 9 t - t^{2} + C_{1} \end{aligned}$

بما أن السرعة المتجهة الابتدائية هي 2 m/s ، فإن v(0) = 2 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C₁ .

$\begin{aligned} v (t) = 9 t - t^{2} + C_{1} \\ 2 = 9 (0) - (0)^{2} + C_{1} \\ C_{1} = 2 \\ v (t) = 9 t - t^{2} + 2 \\ s (t) = \int v (t) d t \\ = \int (9 t - t^{2} + 2) d t \\ = \frac{1}{2} t^{2} - \frac{1}{3} t^{3} + 2 t + C_{2} \end{aligned}$

بما أن الحركة من نقطة الأصل، فإن s(0) = 0 ، وهذا يُعدّ شرطاً أولياً لإيجاد قيمة ثابت التكامل C₂ .

$\begin{aligned} s (t) = \frac{1}{2} t^{2} - \frac{1}{3} t^{3} + 2 t + C_{2} \\ 0 = \frac{1}{2} (0)^{2} - \frac{1}{3} (0)^{3} + 2 (0) + C_{2} \\ C_{2} = 0 \\ s (t) = \frac{1}{2} t^{2} - \frac{1}{3} t^{3} + 2 t \\ s (2) = \frac{1}{2} (2)^{2} - \frac{1}{3} (2)^{3} + 2 (2) \\ = \frac{58}{3} \end{aligned}$

إذن موقع الجُسيم بعد ثانيتين من بدء الحركة هو: $\frac{58}{3}$ m

إعداد : شبكة منهاجي التعليمية

27 / 01 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025