مهارات التفكير العليا

مهارات التفكير العليا

تكامل اقترانات خاصة

(34) أكتشف الخطأ: أوجد أحمد ناتج التكامل: $\int \frac{1}{2 x} d x$ ، وكان خله على النحو المجاور.

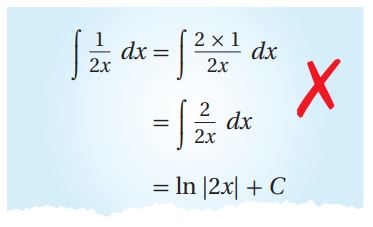
أكتشف الخطأ في حل أحمد، ثم أصححه.

$\begin{aligned} \int \frac{1}{2 x} d x & = \int \frac{\frac{1}{2} (2)}{2 x} d x \\ = \frac{1}{2} \int \frac{2}{2 x} d x \\ = \frac{1}{2} \ln | 2 x | + C \end{aligned}$

تحد: أجد كل تكامل مما يأتي:

$\int \sqrt{e^{x}} d x$ (35)

$\begin{aligned} \int \sqrt{e^{x}} d x & = \int {(e^{x})}^{\frac{1}{2}} d x \\ = \int e^{\frac{1}{2} x} d x \\ = 2 e^{\frac{1}{2} x} + C \end{aligned}$

$\int \frac{\cos x}{3 + 2 \sin x} d x$ (36)

$\begin{aligned} \int \frac{\cos x}{3 + 2 \sin x} d x & = \int \frac{- \frac{1}{2} (- 2 \cos x)}{3 + 2 \sin x} d x \\ = - \frac{1}{2} \int \frac{- 2 \cos x}{3 + 2 \sin x} d x \\ = - \frac{1}{2} \ln | 3 + 2 \sin x | + C \end{aligned}$

$\int {(x^{2} + 2 x + 1)}^{5} d x$ (37)

$\begin{aligned} \int {(x^{2} + 2 x + 1)}^{5} d x & = \int {((x + 1)^{2})}^{5} d x \\ = \int (x + 1)^{10} d x \\ = \frac{1}{11} (x + 1)^{11} + C \end{aligned}$

(38) أكتشف المختلف: أي التكاملات الآتية مختلف، مبرراً إجابتي؟

أكتشف المختلف للسؤال 38

$\int \frac{1}{x + 1} d x$

هذا التكامل هو المختلف $\int \frac{1}{x + 1} d x$ كونه الوحيد الذي يُحل باللوغاريتم الطبيعي.

إعداد : شبكة منهاجي التعليمية

10 / 02 / 2023

حمّل تطبيق منهاجي الجديد

النقاشات

حمّل تطبيق منهاجي الجديد

النقاشات

جميع الحقوق محفوظة © 2025